Question

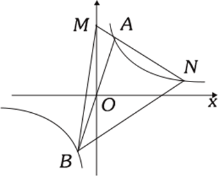
【题目】如图，在平面直角坐标系xOy中，⊙A与y轴相切于点B（0，），与x轴相交于M，N两点，如果点M的坐标为（，0），求点N的坐标

Answer 1

【答案】N(, 0)．

【解析】

试题连接AB、AM、过A作AC⊥MN于C，设⊙A的半径是R，根据切线性质得出AB=AM=R，求出CM=R-，AC=，MN=2CM，

由勾股定理得出方程R2=（R-）2+（）2，求出方程的解即可．

试题解析：连接AB、AM、过A作AC⊥MN于C，设⊙A的半径是R，

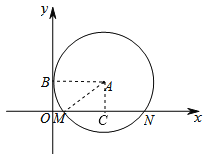
∵⊙A与y轴相切于B，

∴AB⊥y轴，

∵点B（0，），与x轴相交于M、N两点，点M的坐标为（，0），

∴AB=AM=R，CM=R-，AC=，MN=2CM，

由勾股定理得：R2=（R-）2+（）2，

R=2．5，

∴CM=CN=2．5-=2，

∴ON=+2+2=4，

即N的坐标是（4，0）．