Question

【题目】如图，已知抛物线y＝x2＋bx＋c过点A(3, 0)、点B(0, 3)．点M(m, 0)在线段OA上（与点A、O不重合），过点M作x轴的垂线与线段AB交于点P，与抛物线交于点Q，联结BQ．

（1）求抛物线表达式；

（2）联结OP，当∠BOP＝∠PBQ时，求PQ的长度；

（3）当△PBQ为等腰三角形时，求m的值．

Answer 1

【答案】(1) y＝x2＋2x＋3；(2) ；(3) m的值为2、或1.

【解析】

（1）将点A (3, 0)、点B (0, 3) 分别代入抛物线解析式y＝x2＋bx＋c，化简求出b，c的值即可；

（2）根据∠BOP ＝∠PBQ且MQ∥OB，可证△OBP ∽△BPQ，可设Q（x，x2＋2x＋3），求出直线AB的解析式，则可得P 的坐标为(x，3－x)，可得BP＝x，OB＝3，PQ＝x2＋3x，利用相似三角形的对应边成立比例即可求解；

（3）分三种情况讨论：①当BQ＝PQ时，②当BP＝PQ时，③当BP＝BQ时，然后分别求解即可.

（1）∵将点A (3, 0)、点B (0, 3) 分别代入抛物线解析式y＝x2＋bx＋c得

，解之得：

∴抛物线的解析式为y＝x2＋2x＋3

（2）

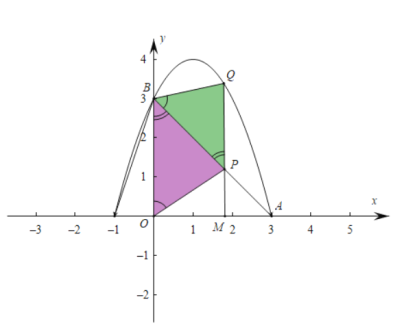
∵∠BOP ＝∠PBQ且MQ∥OB

∴∠OBP ＝∠BPQ

∴△OBP ∽△BPQ

设Q（x，x2＋2x＋3）

∵P点在直线AB上，并A (3, 0)、B (0, 3)，

则直线AB的解析式为：

∴ P (x，3－x)

∴BP＝x，OB＝3，PQ＝x2＋3x

∴ 即

∴（0舍去）

∴

（3）∵M（m，0），P（m，3－m），Q（m，m2＋2m＋3）

∴BP＝m，PQ＝m2＋3m且∠BPQ＝45°

∴当△BPQ为等腰三角形时，存在如下情况：

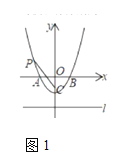
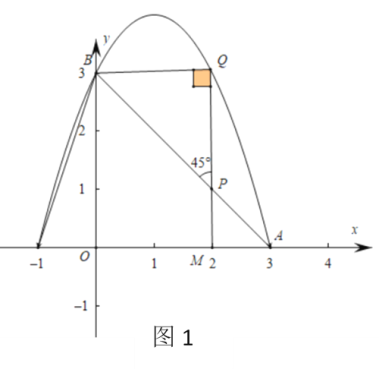
①如图1，当BQ＝PQ时，即∠PBQ＝∠BPQ＝45°

∴△BPQ为等腰直角三角形 ∴m2＋2m＋3＝3

∴m＝2

②当BP＝PQ时,即m＝m2＋3m，即（0舍去）

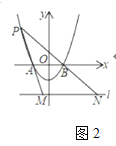
③如图2，当BP＝BQ时，∠BQP＝∠BPQ＝45°

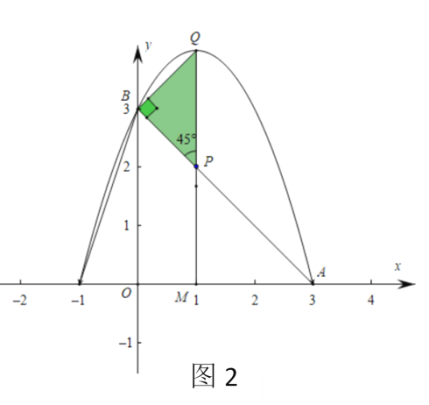
根据，，可得

则有 ，

∴m＝1

综上所述，m的值为2、或1.