Question

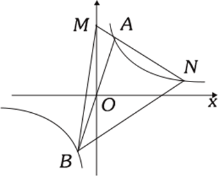
【题目】如图，等腰直角△ABC中，∠ABC＝90°，点P在AC上，将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ．

（1）求∠PCQ的度数；

（2）当AB＝4，AP＝时，求PQ的大小；

（3）当点P在线段AC上运动时（P不与A，C重合），求证：2PB2＝PA2+PC2

Answer 1

【答案】（1）90°；（2）2；（3）见解析

【解析】

（1）先由旋转得出△ABP≌△CBQ，即：∠A=∠ACB=∠BCQ=45°，即可得出结论；

（2）先求出AC，进而求出PC，最后用勾股定理即可得出结论；

（3）先判断出△BPQ是等腰直角三角形，△PCQ是直角三角形，最后用勾股定理即可得出结论．

（1）∵△ABC是等腰直角三角形，

∴∠A＝∠ACB＝45°，

∵△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ．

∴△ABP≌△CBQ，

∴∠A＝∠ACB＝∠BCQ＝45°，

∴∠PCQ＝∠ACB+∠BCQ＝45°+45°＝90°；

（2）在等腰直角三角形ABC中，

∵AB＝4，

∴AC＝4，

∵AP＝，

∴PC＝AC﹣AP＝4﹣＝3，

由（1）知，△ABP≌△CBQ，

∴CQ＝AP＝，

由（1）知，∠PCQ＝90°，

根据勾股定理得，PQ＝＝＝2；

（3）证明：由（1）知，△ABP≌△CBQ，

∴∠ABP＝∠CBQ，AP＝CQ，PB＝BQ

∴∠CBQ+∠PBC＝∠ABP+∠PBC＝90°，

∴△BPQ是等腰直角三角形，△PCQ是直角三角形，

∴PQ＝PB，

∵AP＝CQ，

在Rt△PCQ中，根据勾股定理得，PQ2＝PC2+CQ2＝PA2+PC2

∴2PB2＝PA2+PC2．