题目内容
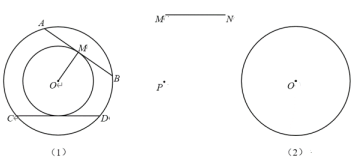
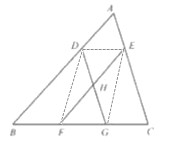
【题目】如图,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.

(1)求证:![]() ;
;
(2)连接![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据已知条件先证明DG∥AC,EF∥AB,可得∠HGF=∠C,∠HFG=∠B,即可证明△HFG∽△ABC,从而可得结论;
(2)连接DF,EG,DE,证明四边形DFGE和ADHE是平行四边形,即可证得结论.
∵AB=3AD,BF=FG=CG,
∴BD=2AD,BG=2CG,
∴![]() ,
,
∴DG∥AC,
同理可得,EF∥AB,
∴∠HFG=∠ABC,∠HGF=∠ACB,
∴△HFG∽△ABC,
∴![]() ,即
,即![]() ;
;
(2)连接![]() ,DE,如图所示,
,DE,如图所示,
∵EF∥AB,
∴![]() ,
,
∵GF=FB
∴![]() =1,
=1,
∴GH=HD,
同理可证,FH=EH,
∴四边形DFGE是平行四边形,
∴DF∥EG,
∴∠FDG=∠EGD,
∴∠FHG=∠EGH+∠HEG,
∵∠DHE=∠FHG,
∴∠DHE=∠EGH+∠HEG=![]() ,
,
由EF∥AB,DG∥AC,得四边形ADHE是平行四边形,
∴∠A=∠DHE,
∴![]()

练习册系列答案
相关题目
【题目】某商店购进了一种新款小电器,为了寻找合适的销售价格,进行了为期5周的试营销,试营销的情况如表所示:
第1周 | 第2周 | 第3周 | 第4周 | 第5周 | |
售价/(元/台) | 50 | 40 | 60 | 55 | 45 |
销售/台 | 360 | 420 | 300 | 330 | 390 |
已知该款小电器的进价每台30元,设该款小电器每台的售价为x元,每周的销量为y台.
(1)观察表中的数据,推断y与x满足什么函数关系,并求出这个函数关系式;
(2)若想每周的利润为9000元,则其售价应定为多少元?
(3)若每台小电器的售价不低于40元,但又不能高于进价的2倍,则如何定价才能更快地减少库存?此时每周最多可销售多少台?