题目内容
【题目】在平面直角坐标系![]() 中,给出如下定义:若点
中,给出如下定义:若点![]() 在图形
在图形![]() 上,点
上,点![]() 在图形
在图形![]() 上,如果
上,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 的“近距离”,记为
的“近距离”,记为![]() .特别地,当图形
.特别地,当图形![]() 与图形
与图形![]() 有公共点时,
有公共点时,![]() .
.
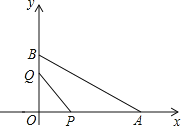
已知![]() ,
,![]() ,
,![]() ,
,
(1)![]() 点
点![]() ,点
,点![]()
![]() ,
,![]() 点
点![]() ,线段
,线段![]()
![]() ;
;
(2)⊙![]() 半径为
半径为![]() ,
,
①当![]() 时,求⊙
时,求⊙![]() 与线段
与线段![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,线段
,线段![]() ;
;
②若![]() ⊙
⊙![]() ,
,![]()
![]() ,则
,则![]() .
.
(3)![]() 为
为![]() 轴上一点,⊙
轴上一点,⊙![]() 的半径为1,点
的半径为1,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,⊙
,⊙![]() 与
与![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,
,![]() ,请直接写出圆心
,请直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,2;(2)①
,2;(2)①![]() ;②
;②![]() 或5;(3)
或5;(3)![]()
【解析】
(1) 根据图形M,N间的“距离”的定义即可解决问题;(2) ①设P为⊙O上一点,Q为线段AB上一点,根据当O、P、Q共线时,PQ最小求解即可; ②利用圆外一点到圆上的最近距离即可确定出半径的范围;(3)分两种种情形分别求解即可解决问题.
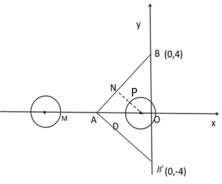
(1)如图所示:
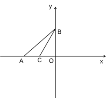
![]() 点
点![]() ,点
,点![]()
![]()
![]() ,
,![]() 点
点![]() ,线段
,线段![]() =4-2=2;
=4-2=2;
(2)①作OD⊥AB交AB于D,交⊙O于点E,OD=![]() ,
,
∴![]() ⊙
⊙![]() ,线段
,线段![]() =DE=2
=DE=2![]() -1,
-1,
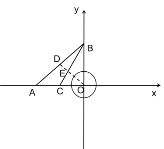
②若![]() ⊙
⊙![]() ,
,![]() =
=![]() ⊙
⊙![]() ,
,![]() 时,
时,![]() ⊙
⊙![]() ,
,![]() =
=![]() ,
,![]() ;
;
若![]() ⊙
⊙![]() ,
,![]() =
=![]() ⊙
⊙![]() ,
,![]() 时,
时,![]() ⊙
⊙![]() ,
,![]() =MN=
=MN=![]() ,∴r的值为
,∴r的值为![]() 或5;
或5;
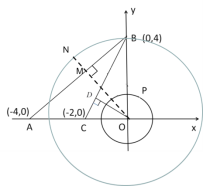
(3)![]()
①D在A点左侧时,近距离为AM的长;
②D在A点右侧时,近距离为PN垂线段的长.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目