ΧβΡΩΡΎ»ί
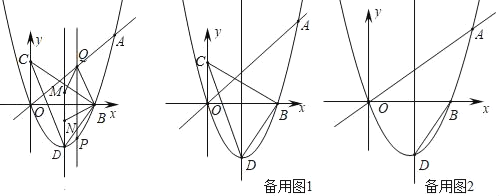
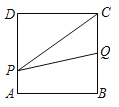
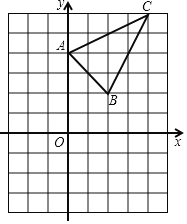
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC‘ΎΉχ±ξΤΫΟφΡΎΘ§»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣAΘ®0Θ§4Θ©Θ§BΘ®2Θ§2Θ©Θ§CΘ®4Θ§6Θ©Θ®’ΐΖΫ–ΈΆχΗώ÷–Θ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ1Θ©
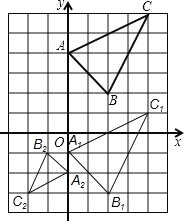
Θ®1Θ©Μ≠≥ωΓςABCœρœ¬ΤΫ“Τ5ΗωΒΞΈΜΒΟΒΫΒΡΓςA1B1C1Θ§≤Δ–¥≥ωΒψB1ΒΡΉχ±ξΘΜ
Θ®2Θ©“‘ΒψOΈΣΈΜΥΤ÷––ΡΘ§‘ΎΒΎ»ΐœσœόΜ≠≥ωΓςA2B2C2Θ§ ΙΓςA2B2C2”κΓςABCΈΜΥΤΘ§«“ΈΜΥΤ±»ΈΣ1ΘΚ2Θ§÷±Ϋ”–¥≥ωΒψC2ΒΡΉχ±ξΚΆΓςA2B2C2ΒΡΟφΜΐΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘ§Θ®2Θ§©¹3Θ©ΘΜ
Θ®2Θ©ΦϊΫβΈωΘ§1.5.
ΓΨΫβΈωΓΩ
Θ®1Θ©÷±Ϋ”άϊ”ΟΤΫ“ΤΒΡ–‘÷ ΒΟ≥ωΕ‘”ΠΒψΈΜ÷ΟΫχΕχΒΟ≥ω¥πΑΗΘΜ
Θ®2Θ©÷±Ϋ”άϊ”ΟΈΜΥΤΆΦ–ΈΒΡ–‘÷ ΒΟ≥ωΕ‘”ΠΒψΈΜ÷ΟΫχΕχΫαΚœ»ΐΫ«–ΈΟφΜΐ«σΖ®ΒΟ≥ω¥πΑΗΘ°
ΫβΘΚΘ®1Θ©»γΆΦΥυ ΨΘΚΓςA1B1C1Θ§Φ¥ΈΣΥυ«σΘΜ
ΒψB1ΒΡΉχ±ξΈΣΘΚΘ®2Θ§©¹3Θ©ΘΜ
Θ®2Θ©»γΆΦΥυ ΨΘΚΓςA2B2C2Θ§Φ¥ΈΣΥυ«σΘΜ
ΒψC2ΒΡΉχ±ξΈΣΘΚΘ®©¹2Θ§©¹3Θ©ΘΜ
ΓςA2B2C2ΒΡΟφΜΐΈΣΘΚ4©¹![]() ΓΝ1ΓΝ1©¹
ΓΝ1ΓΝ1©¹![]() ΓΝ1ΓΝ2©¹
ΓΝ1ΓΝ2©¹![]() ΓΝ1ΓΝ2ΘΫ1.5Θ°
ΓΝ1ΓΝ2ΘΫ1.5Θ°
 .
.

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
œύΙΊΧβΡΩ