��Ŀ����
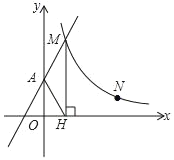
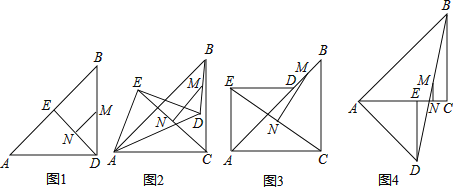
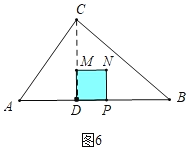
����Ŀ������ABC�У�AC��5��AB��7��BC��4![]() ����D�ڱ�AB�ϣ���AD��3������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������PDMN�����P�˶���ʱ��Ϊt��������PDMN����ABC�ص����ֵ����ΪS��
����D�ڱ�AB�ϣ���AD��3������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������PDMN�����P�˶���ʱ��Ϊt��������PDMN����ABC�ص����ֵ����ΪS��
��1���ú���t�Ĵ���ʽ��ʾ�߶�PD�ij�
��2������N������ABC�ı���ʱ����t��ֵ
��3����S��t�ĺ�����ϵʽ
��4������P���߶�AD���˶�ʱ������N����CD�ĶԳƵ�N������N������ABC��ijһ������������ֱ��ƽ����ABC�����ʱ����t��ֵ��
���𰸡���1����0��t��3ʱ��PD��3��t����3��t��7ʱ��PD��t��3����2������������t��ֵΪ![]() s��5s����3��
s��5s����3��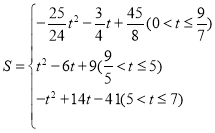 ����4������������t��ֵΪ1s��
����4������������t��ֵΪ1s��![]() s��
s��![]() s��
s��
��������
��1���������������0��t��3ʱ��PD��3��t����3��t��7ʱ��PD��t��3��
��2�����ݣ�1�����������������ƽ�з��߶γɱ��������������t��ֵ��
��3��������PDMN����ABC�ص����ֵ���״����Ϊ����Ρ������Ρ�����Σ�
�ɷ����ηֱ���
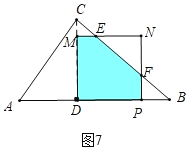
����ͼ4�У���0��t��![]() ʱ���ص������������EFPDM��
ʱ���ص������������EFPDM��
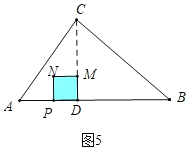
����ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN��
��t��5ʱ���ص�������������PDMN��
����ͼ7�У���5��t��7ʱ���ص������������EFPDM��
����ƽ�з��߶γɱ����������ֱ���S��t�ĺ�����ϵʽ��
��4�����������������֪��N����CD�ĶԳƵ�N������AC��BC��AB���ߵ������ϣ�
���������,����ͼ�Σ�����ƽ���߷��߶γɱ��������������̼��ɽ�����⣮
��1����ͼ1�У���CD���AB��D��
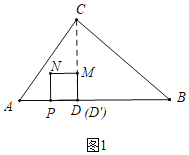
��![]() ����
����![]()
�ɹ��ɶ����ã�![]() ��
��![]() ��
��
![]()
��ã�![]() ����
����![]()
��0��t��3ʱ��PD��3��t��
��3��t��7ʱ��PD��t��3��
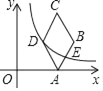
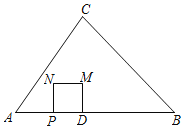
��2������ͼ2�У�����N��AC��ʱ��
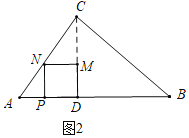
��MN��AD��
![]()
![]()
���![]() .
.
����ͼ3�У�����N��BC��ʱ��
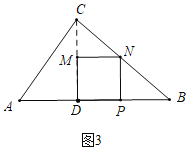
��MN��BD��
![]()
![]()
���t��5
��������������������t��ֵΪ![]() s��5s��
s��5s��
��3��������PDMN����ABC�ص����ֵ��������Ϊ����Ρ������Ρ�����Σ����Է�����������ۣ�
����ͼ4�У���0��t��![]() ʱ���ص������������EFPDM��
ʱ���ص������������EFPDM��
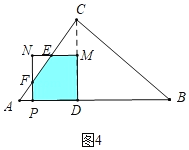
s��S������MDPN��S��NEF����3��t��2��![]()
![]() ��3��t��
��3��t��![]() t��2��
t��2��![]() ��
��
����ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN��s��t2��6t+9
��t��5ʱ���ص�������������PDMN��s��t2��6t+9
����ͼ7�У���5��t��7ʱ���ص������������EFPDM��s��S������MNPD��S��EFN����t��3��2��![]() [��t��3������7��t��]2����t2+14t��41��
[��t��3������7��t��]2����t2+14t��41��
����������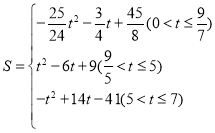 ��
��
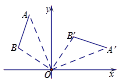
��4��N����CD�ĶԳƵ�N������ABC��ijһ������������ֱ��ƽ����ABC�����,
��N��������ABC�������ϣ����Է�����������ۣ�
��ͼ8�У�����N����������AE��ʱ����EK��BC��K��N��J��AB��J��
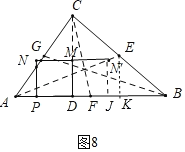
��JN���EK��
![]() ,
,
����![]() ��
��
���t��1��
��ͼ9�У�����N����������BG��ʱ����GK��BC��K��N��J��AB��J��
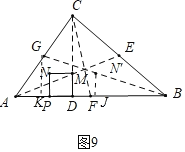
��N��J��GK��
![]() ,
,
![]()
���![]()
��ͼ10�У�����N����������CF��ʱ��
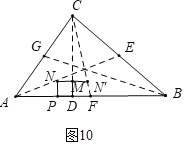
��MN���DF��
![]() ,
,
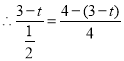 ��
��
���![]()
��������������������t��ֵΪ1s��![]() s��
s��![]() s��
s��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�