题目内容
【题目】某游乐园要建一个圆形喷水池,在喷水池的中心安装一个大的喷水头,高度为![]() m,喷出的水柱沿抛物线轨迹运动(如图),在离中心水平距离4m处达到最高,高度为6m,之后落在水池边缘,那么这个喷水池的直径AB为____m.
m,喷出的水柱沿抛物线轨迹运动(如图),在离中心水平距离4m处达到最高,高度为6m,之后落在水池边缘,那么这个喷水池的直径AB为____m.

【答案】20
【解析】
根据题意在离中心水平距离4m处达到最高,高度为6m,设顶点式解析式,求出解析式,再求出与x轴的交点坐标即可求出这个喷水池的直径AB.
∵喷出的水柱中心4m处达到最高,高度为6m,
∴抛物线的顶点坐标为(4,6)或(4,6),
设抛物线解析式为![]() 或
或![]()
即这个喷水头应设计的高度为![]() m.
m.
把![]() 代入抛物线解析式,解得:
代入抛物线解析式,解得:![]()
所以,函数解析式为![]() 或
或![]()
当![]() 时, 抛物线与x轴的交点坐标为(10,0)或(10,0),
时, 抛物线与x轴的交点坐标为(10,0)或(10,0),
∴圆形喷水池的直径为20m,
故答案为:20.

【题目】某数学兴趣小组在探究函数y=x2﹣2|x|+3的图象和性质时,经历了以下探究过程:
(1)列表(完成下列表格).
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | 0 |
| 1 | 2 | 3 | … |
y | … | 6 | 3 | 2 |
|
|
| 2 | 3 | 6 | … |
(2)描点并在图中画出函数的大致图象;
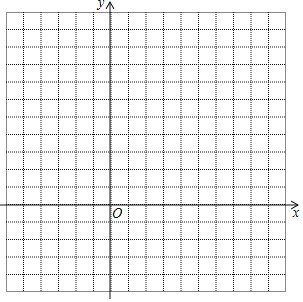
(3)根据函数图象,完成以下问题:
①观察函数y=x2﹣2|x|+3的图象,以下说法正确的有 (填写正确的序号)
A.对称轴是直线x=1;
B.函数y=x2﹣2|x|+3的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
C.当﹣1<x<1时,y随x的增大而增大;
D.当函数y=x2﹣2|x|+3的图象向下平移3个单位时,图象与x轴有三个公共点;
E.函数y=(x﹣2)2﹣2|x﹣2|+3的图象,可以看作是函数y=x2﹣2|x|+3的图象向右平移2个单位得到.
②结合图象探究发现,当m满足 时,方程x2﹣2|x|+3=m有四个解.
③设函数y=x2﹣2|x|+3的图象与其对称轴相交于P点,当直线y=n和函数y=x2﹣2|x|+3图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,求n的值.
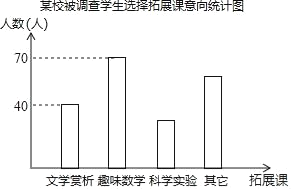
【题目】为丰富学生的课余生活,某校记划开展三种拓展课活动,分别是“文学赏析”,“趣味数学”,“科学实验”等项目,要求每位学生自主选择其中一项拓展课参加.随机抽取该校各年段部分学生,对选择拓展课的意向进行调査,将调查的结果制作成以下统计图和不完整的统计表.
某校被调查学生选择拓展课意向统计表
选择意向 | 所占百分比 |
文学赏析 |
|
趣味数学 | 35% |
科学实验 |
|
其它 | 30% |
(1)该校有2000名学生,请你估计大约有多少名学生参加科学实验拓展课,并补全统计表.
(2)该校参加科学实验拓展课的学生随机分成A,B,C三个人数相同的班级.小慧和小明都参加科学实验拓展课,求他们同班级的概率(画树状图或列表法求解)