题目内容
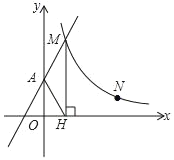
【题目】如图，直线y＝2x+2与y轴交于A点，与反比例函数y＝
（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO＝2．
（1）求H点的坐标及k的值；
（2）点P在y轴上，使△AMP是以AM为腰的等腰三角形，请直接写出所有满足条件的P点坐标；
（3）点N（a，1）是反比例函数y＝（x＞0）图象上的点，点Q（m，0）是x轴上的动点，当△MNQ的面积为3时，请求出所有满足条件的m的值．
【答案】（1）k＝4；（2）点P的坐标为（0，6）或（0，2+
），或（0，2﹣）；（3）m＝7或3．
【解析】
（1）先求出OA=2，结合tan∠AHO=2可得OH的长，即可得知点M的横坐标，代入直线解析式可得点M坐标，代入反比例解析式可得k的值；
（2）分AM=AP和AM=PM两种情况分别求解可得；
（3）先求出点N（4，1），延长MN交x轴于点C，待定系数法求出直线MN解析式为y=-x+5．据此求得OC=5，再由S△MNQ=S△MQC-S△NQC=3知QC=2，再进一步求解可得．
（1）由y＝2x+2可知A（0，2），即OA＝2，
∵tan∠AHO＝2，
∴OH＝1，
∴H（1，0），
∵MH⊥x轴，
∴点M的横坐标为1，
∵点M在直线y＝2x+2上，
∴点M的纵坐标为4，即M（1，4），
∵点M在y＝
上，
∴k＝1×4＝4；
（2）①当AM＝AP时，
∵A（0，2），M（1，4），
∴AM＝，
则AP＝AM＝，
∴此时点P的坐标为（0，2﹣）或（0，2+）；
②若AM＝PM时，
设P（0，y），
则PM＝
，
∴＝，
解得y＝2（舍）或y＝6，
此时点P的坐标为（0，6），
综上所述，点P的坐标为（0，6）或（0，2+），或（0，2﹣）；
（3）∵点N（a，1）在反比例函数y＝
（x＞0）图象上，
∴a＝4，
∴点N（4，1），
延长MN交x轴于点C，
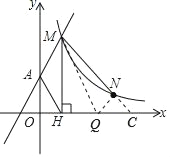
设直线MN的解析式为y＝mx+n，
则有
解得
，
∴直线MN的解析式为y＝﹣x+5．
∵点C是直线y＝﹣x+5与x轴的交点，
∴点C的坐标为（5，0），OC＝5，
∵S△MNQ＝3，
∴S△MNQ＝S△MQC﹣S△NQC＝
×QC×4﹣×QC×1＝
QC＝3，
∴QC＝2，
∵C（5，0），Q（m，0），
∴|m﹣5|＝2，
∴m＝7或3，
故答案为：7或3．
