题目内容
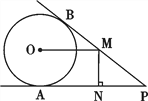
【题目】如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
【答案】(1)证明见解析;(2)5.
【解析】试题分析:(1)连接OA,由切线的性质可知OA⊥AP,再由MN⊥AP可知四边形ANMO是矩形,故可得出结论;
(2)连接OB,则OB⊥BP由OA=MN,OA=OB,OM∥AP.可知OB=MN,∠OMB=∠NPM.故可得出Rt△OBM≌△MNP,OM=MP.设OM=x,则NP=9-x,在Rt△MNP利用勾股定理即可求出x的值,进而得出结论.
试题解析:(1)如图,连接OA,则OA⊥AP,

∵MN⊥AP,
∴MN∥OA,
∵OM∥AP,
∴四边形ANMO是矩形,
∴OM=AN;
(2)解:连接OB,则OB⊥BP
∵OA=MN,OA=OB,OM∥AP.
∴OB=MN,∠OMB=∠NPM.
∴Rt△OBM≌Rt△MNP,
∴OM=MP.
设OM=x,则NP=9-x,
在Rt△MNP中,有x2=32+(9-x)2
∴x=5,即OM=5.

练习册系列答案
相关题目