��Ŀ����
����Ŀ����֪����Rt��ABC�͵���Rt��AED�У���ACB=��AED=90�㣬��AD=AC
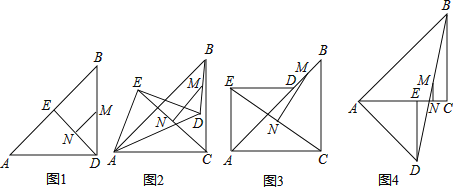
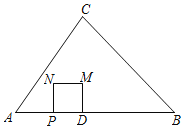
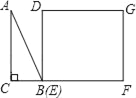
��1�����֣���ͼ1������E��AB���ҵ�C�͵�D�غ�ʱ������M��N�ֱ���DB��EC���е㣬��MN��EC��λ�ù�ϵ���� ����MN��EC��������ϵ���� ��
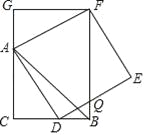
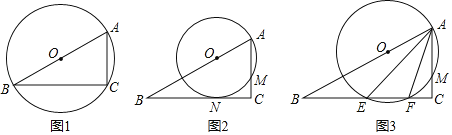
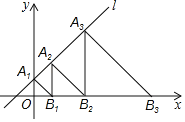
��2��̽�������ѣ�1��С���еġ�AED�Ƶ�A��תһ���Ƕȣ���ͼ2��ʾ������BD��EC��������DB��EC���е�M��N����MN��EC��λ�ù�ϵ��������ϵ��Ȼ�ܳ�������������������ʱ����ת45��õ���ͼ�Σ�ͼ3��Ϊ������֤��λ�ù�ϵ��������˳ʱ����ת45��õ���ͼ�Σ�ͼ4��Ϊ������֤��������ϵ������������������˵�����ɣ�
���𰸡���1��![]() ����2��������������.
����2��������������.
��������
��1�����õ���ֱ�������ε������Լ���������λ�߶����ó��ó�MN��EC��λ�ù�ϵ��MN��EC��������ϵ��
��2�����ȵó���EDM�ա�FBM��SAS�������������EAC�ա�FBC��SAS�������ɵó���ECF=��FCB+��BCE=��ECA+��BCE=90���������ó�MN��EC�������á�EDM�ա�FBM��AAS�����ó���MN��EC��������ϵ��
�⣺��1��![]() ���������£�
���������£�
�ߵ���E��AB���ҵ�C�͵�D�غ�ʱ����M��N�ֱ���DB��EC���е㣬
��MN��������BED����λ�ߣ�
��MN��BE��MN=![]() BE��
BE��
�ߵ���Rt��ABC�͵���Rt��AED�У���ACB=��AED=90������AD=AC��
��BE=EC����AED=90����
��MN��EC��λ�ù�ϵ�ǣ�MN��EC��MN��EC��������ϵ�ǣ�MN=![]() EC��
EC��
�ʴ�Ϊ��MN��EC��MN=![]() EC��
EC��
��2��![]() ���������£�
���������£�
����ͼ������EM���ӳ���F��ʹEM=MF������CM��CF��BF��
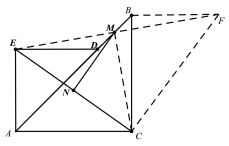
��BM=MD����EMD=��BMF��
���EDM�ա�FBM��SAS����
��BF=DE=AE����FBM=��EDM=135����
���FBC=��EAC=90����
��AC��BC��
���EAC�ա�FBC��SAS����
��FC=EC, ��FCB=��ECA��
���ECF=��FCB+��BCE =��ECA+��BCE=90��
�ֵ�M��N�ֱ���EF��EC���е�
��MN��FC��
��MN��EC��
������ͼ��ʾ������EM���ӳ���BC��F��
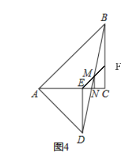
�ߡ�AED=��ACB=90����
��DE��BC��
���DEM=��BFM����EDM=��MBF��
�ڡ�EDM�͡�FBM�У�
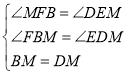 ��
��
���EDM�ա�FBM��AAS����
��BF=DE=AE��EM=FM��
��![]() .
.

 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�