题目内容
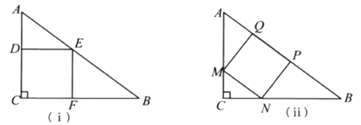
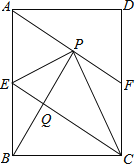
【题目】如图,矩形ABCD中,点E为AB中点,连接CE,将顶点B沿CE折叠至点P处,连接AP并延长交边CD于点F,
(1)判断四边形AECF为的形状并说明理由;
(2)若点P同时可看作是B点绕C点顺时针旋转60°得到,求证:△APB≌△ECP;
(3)若AB=6,BC=4,求![]() 的值
的值

【答案】(1)详见解析;(2详见解析;(3)![]() .
.
【解析】试题分析:(1)由折叠的性质与点E为AB的中点,易得AE=EB=PE,
![]() 即可证得
即可证得![]() 则可得AF∥EC,又由AE∥FC,可证得四边形AECF为平行四边形;
则可得AF∥EC,又由AE∥FC,可证得四边形AECF为平行四边形;
(2)由旋转的性质,易得![]() 是等边三角形,可得
是等边三角形,可得![]() 然后由
然后由![]() 证得:
证得: ![]()
(3)首先利用勾股定理求得![]() 的长,然后利用直角三角形的面积,求得
的长,然后利用直角三角形的面积,求得![]() 的长,即可求得
的长,即可求得![]() 的长,又由勾股定理,求得
的长,又由勾股定理,求得![]() 的长,继而求得
的长,继而求得![]() 的长,则可求得答案.
的长,则可求得答案.
试题解析:(1)四边形AECF为平行四边形。
证明:由折叠得到BE=PE,EC⊥PB,
∵E为AB的中点,
∴AE=EB=PE,
∴AP⊥BP,
![]()
∵四边形ABCD是矩形,
![]()
∴四边形AECF为平行四边形;
(2)∵点P同时可看作是B点绕C点顺时针旋转![]() 得到,
得到,
![]()
∴△PBC是等边三角形,
![]()
由折叠的性质可得: ![]()
![]()
![]()
在△ABP和△ECP中,
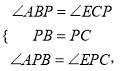
![]()
(3)设BP与CE相较于点Q,
在![]() 中,
中, ![]()
![]()
![]()
![]()
由折叠得: ![]()
在![]() 中,
中, ![]()
∵四边形AECF为平行四边形,
![]()
![]()
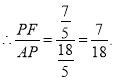

 名校课堂系列答案
名校课堂系列答案【题目】随着地面公交和共享单车的发展,“公交车+单车”的方式已成为很多市民出行的选择。小明放学后从寿春中学出发,先乘坐公交车,根据路面交通的拥堵的实际情况,灵活决定在离家较近的A、B、C、D、E中的某一公交站下车,再骑共享单车回家,设他乘公交车的时间y1(单位:分钟)与下车站点到学校距离x(3≤x≤5)(单位:千米)之间函数关系为y1=2x+2,小明骑单车的时间y2(单位:分钟)与x(3≤x≤5)之间的满足二次函数关系,其具体对应值如下表所示:
地铁站 | A | B | C | D | E |
X(千米) | 3 |
| 4 |
| 5 |
Y2(分钟) | 11 |
| 6 |
| 3 |
(1)求y2关于x的函数表达式;
(2)求小明从学校回到家的时间y(单位:分钟)与x的函数表达式;
(3)请通过计算说明:小明应选择在哪一站下公交车,才能使他从学校回家所需的时间最短?并求出最短时间.