题目内容
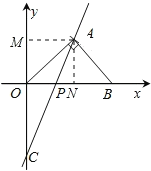
【题目】如图(1),在平面直角坐标系中,等腰直角三角形AOB的斜边OB在x轴上,直线y=2x-2经过等腰直角三角形AOB的直角顶点A,交y轴于点C.
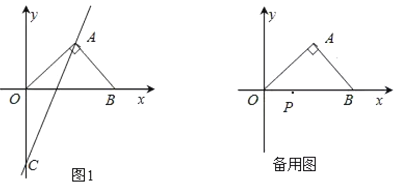
(1)点C坐标是( , );点A坐标是( , );
(2)若D是坐标平面内任意一点,使点A、C、O、D刚好能构成平行四边形,请直接写出符合条件的点D的坐标;
(3)若点P是x轴上一动点.点Q的坐标是(a,![]() ),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
【答案】(1)0,-2,2,2;(2)![]() ,
,![]() ,
,![]() ;(3)a=4,Q(4,1).
;(3)a=4,Q(4,1).
【解析】
(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,根据等腰直角三角形的性质可设点A的坐标为(a,a),再把A点坐标代入y=2x-2,即可算出a的值,进而得到A点坐标,令x=0,代入y=2x-2,即可得到点C的坐标;
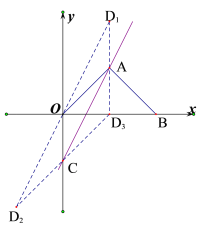
(2)画出草图,根据平行四边形的性质,分3种情况:当以OA为平行四边形的对角线时,当以OC为平行四边形的对角线时,当以AC为平行四边形的对角线时,分别求出点C的坐标,即可;
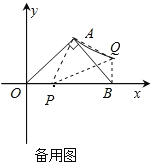
(3)连接AQ,AP,PQ,BQ,由SAS易证△APO≌△AQB,得出∠AOP=∠ABQ=45°,从而求得QB⊥OB,结合B点的坐标,即可得到点Q的坐标.
(1)过点A分别作AM⊥y轴于点M,AN⊥x轴于点N,
∵△AOB是等腰直角三角形,
∴ON=AN=BN,
∵∠MON=∠ANO=∠AMO=90°,
∴四边形ANOM是正方形,
∴AM=AN,
设点A的坐标为(a,a),
∵点A在直线y=2x2上,
∴a=2a2,
解得:a=2,
∴A(2,2),
令x=0,代入y=2x2得:y=-2,
∴C(0,-2).
故答案是:0,-2,2,2;
(2)∵A(2,2),C(0,-2),D是坐标平面内任意一点,使点A、C、O、D刚好能构成平行四边形,
∴当以OA为平行四边形的对角线时,![]() ,当以OC为平行四边形的对角线时,
,当以OC为平行四边形的对角线时,![]() ,当以AC为平行四边形的对角线时,
,当以AC为平行四边形的对角线时,![]() ,
,
综上所述,点D的坐标是:![]() ,
,![]() ,
,![]() ;
;
(3)连接AQ,AP,PQ,BQ,
∵△PAQ是以点A为直角顶点的等腰三角形,
∴AP=AQ,
∵∠OAB=∠PAQ=90°,
∴∠OAB∠PAB=∠PAQ∠PAB,
∴∠OAP=∠BAQ,
在△APO与△AQB中,
∵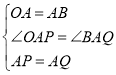 ,
,
∴△APO≌△AQB(SAS),
∴∠AOP=∠ABQ=45°,
∴∠OBQ=45°+45°=90°,
∴QB⊥OB,
∵A(2,2),
由第(1)题,可得OB=2AN=4,
∴B(4,0),
∵Q点的坐标是(a,![]() ),
),
∴a=4,
∴Q(4