题目内容
【题目】已知矩形ABCD,AB=10,BC=13,点P为边AD上一动点,点A’与点A关于BP对称,连结A’C,当△A’BC为等腰三角形时,AP的长度为()

A.2B.![]() C.2或
C.2或![]() D.2或
D.2或![]()
【答案】C
【解析】
①如图1,当A′B=A′C时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,得到MN垂直平分BC和AD,根据轴对称的性质得到AB=A′B=10,∠PA′B=∠A=90°,根据勾股定理得到A′M=![]() ,根据相似三角形的性质即可得到结论;②当A′B=BC时,这种情况不存在;③如图2,当A′C=BC=13时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,由勾股定理得到CH=
,根据相似三角形的性质即可得到结论;②当A′B=BC时,这种情况不存在;③如图2,当A′C=BC=13时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,由勾股定理得到CH=![]() ,根据三角形的面积公式得到A′M=
,根据三角形的面积公式得到A′M=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
解:∵△A′BC为等腰三角形,
∴①如图1,当A′B=A′C时,过A′作A′M⊥BC于M反向延长A′M交AD于N,
则MN⊥AD,
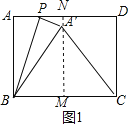
∴MN垂直平分BC和AD,
∵BC=13,
∴BM=AN=![]() ,
,
∵点A′与点A关于BP对称,
∴△ABP≌△A′BP,
∴AB=A′B=10,∠PA′B=∠A=90°,
∴A′M=![]() ,
,
∴A′N=MN-A′M=![]() ,
,
∵∠PA′N+∠A′PN=∠PA′N+∠BA′M=90°,
∴∠A′PN=∠BA′M,
∵∠PNA′=∠A′MB=90°,
∴△A′PN∽△BA′M,
∴![]() ,
,
∴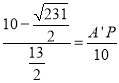 ,
,
∴A′P=![]() ,
,
∴AP=A′P=![]() ,
,
②当A′B=BC时,
∵A′B=AB=10,
∴这种情况不存在;
③如图2,当A′C=BC=13时,
过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,
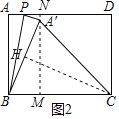
∴BH=![]() ×10=5,
×10=5,
∴CH=![]() ,
,
∴A′M=![]() ,
,
∴A′N=![]() ,BM=
,BM=![]() ,
,
由①知,![]() ,
,
∴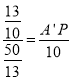 ,
,
∴A′P=AP=2,
综上所述,AP的长度为2或![]() ;
;
故选:C.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案