题目内容
【题目】随着地面公交和共享单车的发展,“公交车+单车”的方式已成为很多市民出行的选择。小明放学后从寿春中学出发,先乘坐公交车,根据路面交通的拥堵的实际情况,灵活决定在离家较近的A、B、C、D、E中的某一公交站下车,再骑共享单车回家,设他乘公交车的时间y1(单位:分钟)与下车站点到学校距离x(3≤x≤5)(单位:千米)之间函数关系为y1=2x+2,小明骑单车的时间y2(单位:分钟)与x(3≤x≤5)之间的满足二次函数关系,其具体对应值如下表所示:
地铁站 | A | B | C | D | E |
X(千米) | 3 |
| 4 |
| 5 |
Y2(分钟) | 11 |
| 6 |
| 3 |
(1)求y2关于x的函数表达式;
(2)求小明从学校回到家的时间y(单位:分钟)与x的函数表达式;
(3)请通过计算说明:小明应选择在哪一站下公交车,才能使他从学校回家所需的时间最短?并求出最短时间.
【答案】(1)y2=x2-12x+38 (3≤x≤5);(2)y=x2-10x+40 (3≤x≤5);(3)15分钟.
【解析】试题分析:(1)设![]() (a≠0),把(3,11),(4,6),(5,3)代入解方程组即可得到结论;
(a≠0),把(3,11),(4,6),(5,3)代入解方程组即可得到结论;
(2)根据“小明从学校回到家的时间y=他乘公交车的时间y1+小明骑单车的时间y2” 解答即可;
(3)根据二次函数的性质解答即可.
试题解析:解:(1)设![]() (a≠0),把(3,11),(4,6),(5,3)代入得:
(a≠0),把(3,11),(4,6),(5,3)代入得:
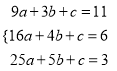 ,解得:
,解得: 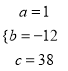 ,∴y2=x2-12x+38 (3≤x≤5);
,∴y2=x2-12x+38 (3≤x≤5);
(2)y=![]() =
=![]() =
=![]() (3≤x≤5);
(3≤x≤5);
(3)![]() .
.
当x≤5时,y随x增大而减小,又3≤x≤5,
∴x=5时,y值最小,此时y最小=15,
故小明应选择E站下公交车,才能使他从学校回家所需的时间最短,最短时间为15分钟.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场计划购进A,B两种新型节能台灯共120盏,这两种台灯的进价、售价如表所示:
类型 价格 | 进价(元/盏) | 售价(元/盏) |
A型 | 30 | 45 |
B型 | 50 | 70 |
(1)若商场预计进货款为5200元,则这两种台灯各购进多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?