题目内容
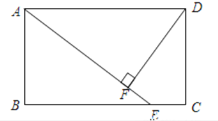
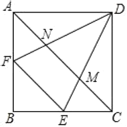
【题目】如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,连结AC,分别交DE,DF于点M,N.
(1)求证:△ADF≌△CDE;
(2)设△DMN和△AFN的面积分别为S1和S2;
①若∠ADF=∠EDF,求S2:S1的值.
②若S2=2S1,求tan∠ADF.
【答案】(1)见解析;(2)①S2:S1的值为![]() ;②tan∠ADF=
;②tan∠ADF=![]() ﹣1.
﹣1.
【解析】
(1)根据HL证明三角形全等即可;
(2)①如图,作NH⊥AB于H.设FH=a.利用参数表示S2,S1即可;
②如图,作NH⊥AB于H.易证∠ADF=∠HNF,设tan∠ADF=tan∠FNH=k,设NH=AH=b,则FH=kb,利用面积关系构建方程求出k即可解决问题.
(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAF=∠DCE=∠ADC=90°,
∵DF=DE,
∴Rt△ADF≌Rt△CDE(HL).
(2)①如图,作NH⊥AB于H.设FH=a.

∵Rt△ADF≌Rt△CDE(HL),
∵∠ADF=∠CDE,
∵∠ADF=∠DEF,
∴∠ADF=∠EDF=∠CDE=30°,
∴∠AFD=60°,
∵∠NHF=90°,
∴∠FNH=30°,
∴HN=![]() a,
a,
∵∠NAH=45°,∠AHN=90°,
∴∠NAH=∠ANH=45°,
∴HA=HN=![]() a,
a,
∴AF=(1+![]() )a,AD=
)a,AD=![]() AF=(3+
AF=(3+![]() )a,
)a,
∴S2=![]() AFNH=
AFNH=![]() (1+
(1+![]() )a
)a![]() a=
a=![]() a2,
a2,
∵∠ADN=∠CDM,AD=DC,∠DAN=∠DCM=45°,
∴△ADN≌△CDM(ASA),
∴S△ADN=S△DCM,
∴S1=S△ADC﹣2S△ADN=![]() [(3+
[(3+![]() )a]2﹣2×
)a]2﹣2×![]() (3+
(3+![]() )a
)a![]() a=(9+6
a=(9+6![]() )a2,
)a2,
∴ .
.
(3)如图,作NH⊥AB于H.

∵∠FHN=∠FAD=90°,
∴HN∥AD,
∴∠ADF=∠HNF,
设tan∠ADF=tan∠FNH=k,设NH=AH=b,则FH=kb,
∴AF=b+kb,
∴AD=![]() ,
,
∴S2=![]() [(1+k)b]2,S1=S△ADC﹣2S△ADN=
[(1+k)b]2,S1=S△ADC﹣2S△ADN=![]() ﹣2×
﹣2×![]() ,
,
∵S2=2S1,
∴![]() (1+k)b]2=2[
(1+k)b]2=2[![]() ﹣2×
﹣2×![]() ]
]
整理得:k2+2k﹣2=0,
解得:k=![]() ﹣1或
﹣1或![]() ﹣1(舍弃),
﹣1(舍弃),
∴tan∠ADF=k=![]() ﹣1.
﹣1.