题目内容
【题目】如图，正方形ABCD的边长为6，点E、F分别在AB、AD上，若CE＝3
，且∠ECF＝45°，则AF的长为（ ）
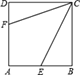
A.4B.3C.2.5D.2
【答案】A
【解析】
延长FD到G，使DG＝BE，连接CG、EF，先利用正方形的性质和SAS证明△BCE≌△DCG，得CE＝CG，再利用SAS证明△GCF≌△ECF，于是GF＝EF，然后利用勾股定理求出BE的长，设AF＝x，在Rt△AEF中利用勾股定理列出方程，解方程即得答案.
解：如图，延长FD到G，使DG＝BE，连接CG、EF；
∵四边形ABCD为正方形，∴BC=DC，∠B=∠CDG=90°，
∴△BCE≌△DCG（SAS），
∴CE＝CG，∠BCE＝∠DCG，
∵∠BCE+∠DCF=45°，∴∠DCG+∠DCF=45°，∴∠GCF＝45°，
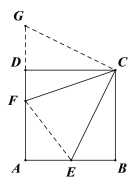
∴∠GCF=∠ECF，又∵CF=CF，∴△GCF≌△ECF（SAS），∴GF＝EF，
∵CE＝3
，CB＝6，∴BE＝
＝3，∴AE＝3，
设AF＝x，则DF＝6﹣x，GF＝3+（6﹣x）＝9﹣x，∴EF＝9﹣x．
在Rt△AEF中，由勾股定理得：（9﹣x）2＝9+x2，
解得：x＝4，即AF＝4．
故选：A．
练习册系列答案
相关题目
