题目内容
【题目】在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
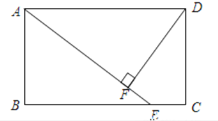
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
【答案】（1）详见解析；（2）8.
【解析】
（1）根据矩形性质得∠AEB=∠DAF，∠DFA=∠B，证ΔADF≌ΔEAB，便可；（2）根据同角的余角相等，∠FDC=∠DAF=30°，故AD=2DF，可进一步求得结果.
证明：在有矩形ABCD中，
∵AD∥BC
∴∠AEB=∠DAF
又∵DF⊥AE，
∴∠DFE=90°．
∴∠DFA=∠B
∵AD=EA
∴ΔADF≌ΔEAB
∴DF=AB．
(2)∵∠ADF+∠FDC=90°，∠DAF+∠ADF=90°
∴∠FDC=∠DAF=30°
∴AD=2DF
∵DF=AB
∴AD=2AB=8.
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
【题目】某公司从2014年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
（1）请你认真分析表中数据，从一次函数和反比例函数中确定哪一个函数能表示其变化规律，给出理由，并求出其解析式；
（2）按照这种变化规律，若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元？
②若打算在2017年把每件产品成本降低到3.2万元，则还需要投入技改资金多少万元？（结果精确到0.01万元）.
