题目内容
【题目】如图，一副三角板的三个内角分别是90°，45°，45°和90°，60°，30°，按如图所示叠放在一起（点A，D，B在同一直线上），若固定△ABC，将△BDE绕着公共顶点B顺时针旋转α度（0＜α＜180），当边DE与△ABC的某一边平行时，相应的旋转角α的值为____．
【答案】45°，75°，165°．
【解析】
分三种情形分别画出图形，利用平行线的性质一一求解即可．
解：①如图1中，当DE∥AB时，
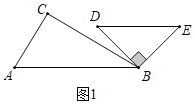
易证∠ABD=∠D=45°，可得旋转角α=45°，
②如图2中，当DE∥BC时，
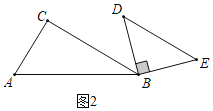
易证∠ABD=∠ABC+∠CBD=∠ABC+∠D=75°，可得旋转角α=75°，
③如图3中，当DE∥AC时，作BM∥AC，
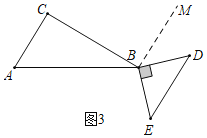
则AC∥BM∥DE，
∴∠CBM=∠C=90°，∠DBM=∠D=45°，
∴∠ABD=30°+90°+45°=165°，可得旋转角α=165°，
综上所述，满足条件的旋转角α为45°，75°，165°
故答案为45°，75°，165°．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
