��Ŀ����
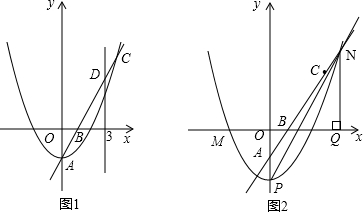
��ͼ1����AΪ������C1��y=
x2-2�Ķ��㣬��B������Ϊ��1��0��ֱ��AB��������C1����һ��C
��1�����C�����ꣻ
��2����ͼ1��ƽ����y���ֱ��x=3��ֱ��AB�ڵ�D����������C1�ڵ�E��ƽ����y���ֱ��x=a��ֱ��AB��F����������C1��G����FG��DE=4��3����a��ֵ��
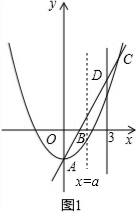
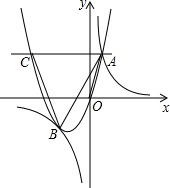
��3����ͼ2����������C1����ƽ��m��m��0������λ�õ�������C2����������C2�Ķ���Ϊ��P����x���ڵ�M��������BC�ڵ�N��NQ��x���ڵ�Q����NPƽ�֡�MNQʱ����m��ֵ��
| 1 |
| 2 |
��1�����C�����ꣻ
��2����ͼ1��ƽ����y���ֱ��x=3��ֱ��AB�ڵ�D����������C1�ڵ�E��ƽ����y���ֱ��x=a��ֱ��AB��F����������C1��G����FG��DE=4��3����a��ֵ��
��3����ͼ2����������C1����ƽ��m��m��0������λ�õ�������C2����������C2�Ķ���Ϊ��P����x���ڵ�M��������BC�ڵ�N��NQ��x���ڵ�Q����NPƽ�֡�MNQʱ����m��ֵ��

��1���ߵ�x=0ʱ��y=-2��
��A��0��-2����
��ֱ��AB�Ľ���ʽΪy=kx+b����
��
���
��ֱ��AB����ʽΪy=2x-2��
�ߵ�CΪֱ��y=2x-2��������y=
x2-2�Ľ��㣬���C�ĺᡢ���������㣺
��
���
��
���ᣩ
���C��������4��6����
��2��ֱ��x=3�ֱ�ֱ��AB��������C1��D��E���㣮
��yD=4��yE=
��
��DE=
��
��FG��DE=4��3��
��FG=2��
��ֱ��x=a�ֱ�ֱ��AB��������C1��F��G���㣮
��yF=2a-2��yG=
a2-2
��FG=|2a-
a2|=2��
��ã�a1=2��a2=2+2
��a3=2-2
��
��3����ֱ��MN��y����T������N��NH��y���ڵ�H��
���M������Ϊ��t��0����������C2�Ľ���ʽΪy=
x2-2-m��
��0=
t2-2-m��
��-2-m=-
t2��
��y=
x2-
t2��
���P������0��-
t2����
�ߵ�N��ֱ��AB��������y=
x2-
t2�Ľ��㣬���N�ĺᡢ���������㣺
��
���
��
���ᣩ��
��N��2-t��2-2t����
NQ=2-2t��MQ=2-2t��
��MQ=NQ��
���MNQ=45�㣮
���MOT����NHT��Ϊ����ֱ�������Σ�
��MO=OT��HT=HN
��OT=-t��NT=
��2-t����PT=-t+
t2��
��PNƽ�֡�MNQ��
���MNP=��PNQ��
��NQ��PT��
���NPT=��PNQ��
���MNP=��NPT��
��PT=NT��
��-t+
t2=
��2-t����
��t1=-2
��t2=2���ᣩ
-2-m=-
t2=-
��-2
��2��
��m=2��
��A��0��-2����
��ֱ��AB�Ľ���ʽΪy=kx+b����
|
���
|
��ֱ��AB����ʽΪy=2x-2��
�ߵ�CΪֱ��y=2x-2��������y=
| 1 |
| 2 |
|
���
|
|
���C��������4��6����

��2��ֱ��x=3�ֱ�ֱ��AB��������C1��D��E���㣮
��yD=4��yE=
| 5 |
| 2 |
��DE=
| 3 |
| 2 |
��FG��DE=4��3��
��FG=2��
��ֱ��x=a�ֱ�ֱ��AB��������C1��F��G���㣮
��yF=2a-2��yG=
| 1 |
| 2 |
��FG=|2a-
| 1 |
| 2 |
��ã�a1=2��a2=2+2
| 2 |
| 2 |
��3����ֱ��MN��y����T������N��NH��y���ڵ�H��

���M������Ϊ��t��0����������C2�Ľ���ʽΪy=
| 1 |
| 2 |
��0=
| 1 |
| 2 |
��-2-m=-
| 1 |
| 2 |
��y=
| 1 |
| 2 |
| 1 |
| 2 |
���P������0��-
| 1 |
| 2 |
�ߵ�N��ֱ��AB��������y=
| 1 |
| 2 |
| 1 |
| 2 |
|
���
|
|
��N��2-t��2-2t����
NQ=2-2t��MQ=2-2t��
��MQ=NQ��
���MNQ=45�㣮
���MOT����NHT��Ϊ����ֱ�������Σ�
��MO=OT��HT=HN
��OT=-t��NT=
| 2 |
| 1 |
| 2 |
��PNƽ�֡�MNQ��
���MNP=��PNQ��
��NQ��PT��
���NPT=��PNQ��
���MNP=��NPT��
��PT=NT��
��-t+
| 1 |
| 2 |
| 2 |
��t1=-2
| 2 |
-2-m=-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
��m=2��

��ϰ��ϵ�д�
�����Ŀ
 A��10��0������OAB�����Ϊ20��
A��10��0������OAB�����Ϊ20��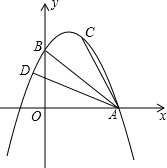

 ��ΪD��
��ΪD��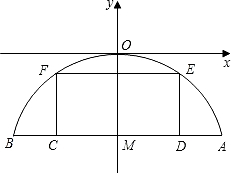 �ϵIJ��ֵĺ�����Ǿ���CDEF����ͼ����ƽ��ֱ������ϵ��
�ϵIJ��ֵĺ�����Ǿ���CDEF����ͼ����ƽ��ֱ������ϵ��