题目内容
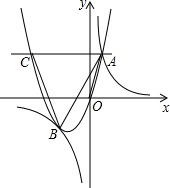
如图,抛物线y=ax2+bx(a>0)与双曲线y=
相交于点A,B.已知点B的坐标为(-2,-2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积?若存在,请你写出点D的坐标;若不存在,请你说明理由.
| k |
| x |
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积?若存在,请你写出点D的坐标;若不存在,请你说明理由.

(1)把点B(-2,-2)的坐标,代入y=
,
得:-2=
,
∴k=4.
即双曲线的解析式为:y=
.
设A点的坐标为(m,n).
∵A点在双曲线上,
∴mn=4.①
又∵tan∠AOx=4,
∴
=4,即n=4m.②
由①②,得:m2=1,
∴m=±1.
∵A点在第一象限,
∴m=1,n=4,
∴A点的坐标为(1,4)
把A、B点的坐标代入y=ax2+bx,得:
,
解得a=1,b=3.
∴抛物线的解析式为:y=x2+3x;
(2)∵AC∥x轴,
∴点C的纵坐标y=4,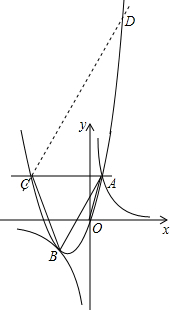
代入y=x2+3x,得方程x2+3x-4=0,
解得x1=-4,x2=1(舍去).
∴C点的坐标为(-4,4),且AC=5,
又∵△ABC的高为6,
∴△ABC的面积=
×5×6=15;
(3)存在D点使△ABD的面积等于△ABC的面积.
过点C作CD∥AB交抛物线于另一点D.
∵△ABD与△ABC同底等高,
∴△ABD的面积等于△ABC的面积,
因为直线AB相应的一次函数是:y=2x+2,且C点的坐标为(-4,4),CD∥AB,
所以直线CD相应的一次函数是:y=2x+12.
解方程组
,
∴x2+3x=2x+12,
即x=3或x=-4,
当x=3时,y=18,
当x=-4时,y=4,
∴
或
(不合题意,舍去),
所以点D的坐标是(3,18).
| k |
| x |
得:-2=
| k |
| -2 |
∴k=4.
即双曲线的解析式为:y=
| 4 |
| x |
设A点的坐标为(m,n).
∵A点在双曲线上,
∴mn=4.①
又∵tan∠AOx=4,
∴
| n |
| m |
由①②,得:m2=1,
∴m=±1.
∵A点在第一象限,
∴m=1,n=4,
∴A点的坐标为(1,4)
把A、B点的坐标代入y=ax2+bx,得:
|
解得a=1,b=3.
∴抛物线的解析式为:y=x2+3x;
(2)∵AC∥x轴,
∴点C的纵坐标y=4,

代入y=x2+3x,得方程x2+3x-4=0,
解得x1=-4,x2=1(舍去).
∴C点的坐标为(-4,4),且AC=5,
又∵△ABC的高为6,
∴△ABC的面积=
| 1 |
| 2 |
(3)存在D点使△ABD的面积等于△ABC的面积.
过点C作CD∥AB交抛物线于另一点D.
∵△ABD与△ABC同底等高,
∴△ABD的面积等于△ABC的面积,
因为直线AB相应的一次函数是:y=2x+2,且C点的坐标为(-4,4),CD∥AB,
所以直线CD相应的一次函数是:y=2x+12.
解方程组
|
∴x2+3x=2x+12,
即x=3或x=-4,
当x=3时,y=18,
当x=-4时,y=4,
∴
|
|
所以点D的坐标是(3,18).

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
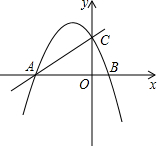
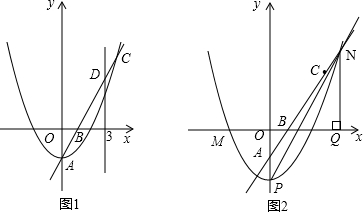
 O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
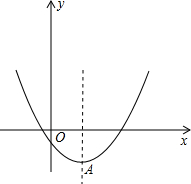
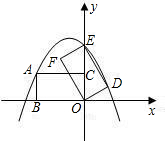 应点为点D,抛物线y=ax2+bx+c过点A,E,D.
应点为点D,抛物线y=ax2+bx+c过点A,E,D.