题目内容
如图,Rt△OAB的斜边OA在x轴的正半轴上,直角的顶点B在第一象限内,已知点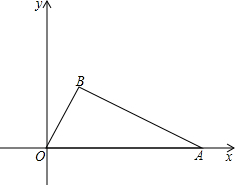 A(10,0),△OAB的面积为20.
A(10,0),△OAB的面积为20.
(1)求B点的坐标;
(2)求过O、B、A三点抛物线的解析式;
(3)判断该抛物线的顶点P与△OAB的外接圆的位置关系,并说明理由.
 A(10,0),△OAB的面积为20.
A(10,0),△OAB的面积为20.(1)求B点的坐标;
(2)求过O、B、A三点抛物线的解析式;
(3)判断该抛物线的顶点P与△OAB的外接圆的位置关系,并说明理由.
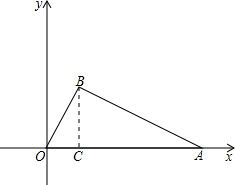
(1)过B作BC⊥OA于C,
∵S△OAB=
OA•BC=20,OA=10,
∴BC=4
在直角三角形ABO中,BC⊥OA,
设OC=x,根据射影定理有:
BC2=OC•AC,即16=x(10-x),解得x=2,x=8
因此B(2,4);
(2)设抛物线的解析式为y=ax(x-10),
已知抛物线过B(2,4),有:
a×2×(2-10)=4,a=-
∴所求的抛物线解析式为:y=-
x2+
x;
(3)由(2)可知:y=-
(x-5)2+
因此P(5,
)
∵
>5
∴顶点P在外接圆外.
∵S△OAB=
| 1 |
| 2 |
∴BC=4
在直角三角形ABO中,BC⊥OA,
设OC=x,根据射影定理有:
BC2=OC•AC,即16=x(10-x),解得x=2,x=8
因此B(2,4);
(2)设抛物线的解析式为y=ax(x-10),
已知抛物线过B(2,4),有:
a×2×(2-10)=4,a=-
| 1 |
| 4 |
∴所求的抛物线解析式为:y=-
| 1 |
| 4 |
| 5 |
| 2 |
(3)由(2)可知:y=-
| 1 |
| 4 |
| 25 |
| 4 |
因此P(5,
| 25 |
| 4 |
∵
| 25 |
| 4 |
∴顶点P在外接圆外.


练习册系列答案
相关题目

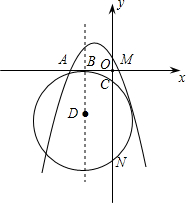
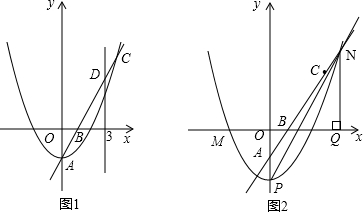
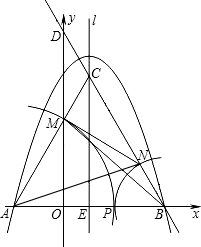 接AN、BM、MN.
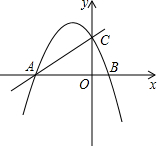
接AN、BM、MN.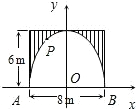 标系中.
标系中.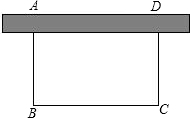 围起,栽上蝴蝶花,共用篱笆x0n,
围起,栽上蝴蝶花,共用篱笆x0n,