题目内容
抛物线y=ax2+bx+c,与x轴交于点A(-3,0),对称轴为x=-1,顶点C到x轴的距离为2,求此抛物线的解析式.
∵抛物线与x轴交于点A(-3,0),对称轴为x=-1,
∴抛物线与x轴的另一个交点坐标为(1,0),
设抛物线的解析式为y=a(x+3)(x-1),
∵顶点C到x轴的距离为2,
∴C点坐标为(-1,2)或(-1,-2),
把(-1,2)代入y=a(x+3)(x-1)得a(-1+3)×(-1-1)=2,解得a=-
,
∴抛物线的解析式为y=-
(x+3)(x-1)=-
x2-x+
;
把(-1,-2)代入y=a(x+3)(x-1)得a(-1+3)×(-1-1)=-2,解得a=
,
∴抛物线的解析式为y=
(x+3)(x-1)=
x2+x-
,
即此抛物线的解析式为y=-
x2-x+
或y=
x2+x-
.
∴抛物线与x轴的另一个交点坐标为(1,0),
设抛物线的解析式为y=a(x+3)(x-1),
∵顶点C到x轴的距离为2,
∴C点坐标为(-1,2)或(-1,-2),
把(-1,2)代入y=a(x+3)(x-1)得a(-1+3)×(-1-1)=2,解得a=-
| 1 |
| 2 |
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
把(-1,-2)代入y=a(x+3)(x-1)得a(-1+3)×(-1-1)=-2,解得a=
| 1 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即此抛物线的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目
 60度.
60度.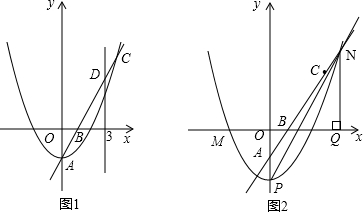
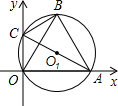
 O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
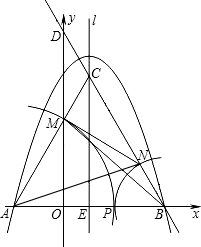 接AN、BM、MN.
接AN、BM、MN. 门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.