题目内容
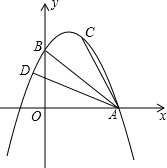
如图,在直角坐标系xOy中,二次函数y=-
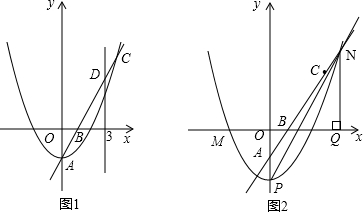
x2+bx+5的图象与x轴、y轴的公共点分别为A(5、0)、B,点C在这个二次函数的图象上,且横坐标为3.
(1)求这个二次函数的解析式;
(2)求∠BAC的正切值;
(3)如果点D在这个二次函数的图象上,且∠DAC=45°,求点D的坐标.
| 2 |
| 3 |
(1)求这个二次函数的解析式;
(2)求∠BAC的正切值;
(3)如果点D在这个二次函数的图象上,且∠DAC=45°,求点D的坐标.

(1)将点A(5,0)代入,可得:0=-
×52+5b+5,
解得:b=
,
故二次函数解析式为y=-
x2+
x+5.
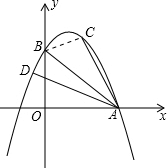
(2)连接BC,
 ,
,
∵抛物线的解析式为y=-
x2+
x+5,
∴点B的坐标为(0,5),
∵点C的横坐标为3,
∴点C的纵坐标为6,即可得点C的坐标为(3,6),
则BC=
=
,AB=5
,AC=
=
,
∵AB2=BC2+AC2,
∴△ABC是直角三角形,
∴tan∠BAC=
=
=
;
(3)∵OA=OB=5,∠BOA=90°,
∴∠BAO=45°,
又∵∠DAC=45°,
∴∠DAO=∠BAC,
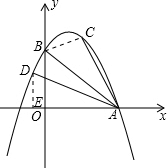
设点D的坐标为(x,-
x2+
x+5),
则tan∠DAO=tan∠BAC=
=
,
解得:x1=-
,x2=5(舍去),
故点D的坐标为(-
,
).
| 2 |
| 3 |
解得:b=
| 7 |
| 3 |
故二次函数解析式为y=-
| 2 |
| 3 |
| 7 |
| 3 |
(2)连接BC,
 ,
,∵抛物线的解析式为y=-
| 2 |
| 3 |
| 7 |
| 3 |
∴点B的坐标为(0,5),
∵点C的横坐标为3,
∴点C的纵坐标为6,即可得点C的坐标为(3,6),
则BC=
| (3-0)2+(6-5)2 |
| 10 |
| 2 |
| (5-3)2+(0-6)2 |
| 40 |
∵AB2=BC2+AC2,
∴△ABC是直角三角形,
∴tan∠BAC=
| BC |
| AC |
| ||
|
| 1 |
| 2 |
(3)∵OA=OB=5,∠BOA=90°,
∴∠BAO=45°,
又∵∠DAC=45°,
∴∠DAO=∠BAC,

设点D的坐标为(x,-
| 2 |
| 3 |
| 7 |
| 3 |
则tan∠DAO=tan∠BAC=
-
| ||||
| 5-x |
| 1 |
| 2 |
解得:x1=-
| 3 |
| 4 |
故点D的坐标为(-
| 3 |
| 4 |
| 23 |
| 8 |

练习册系列答案
相关题目
 -2,0),B(-1,-3).
-2,0),B(-1,-3).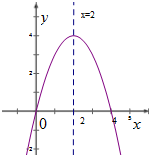

 标系中.
标系中.