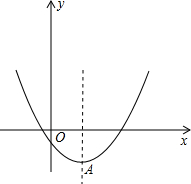题目内容
取一张矩形的纸进行折叠,具体操作过程如下:
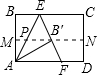
第一步:先把矩形ABCD对折,折痕为MN,如图(1)所示;
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB′E,如图(2)所示;
第三步:沿EB′线折叠得折痕EF,如图(3)所示;利用展开图(4)所示.

探究:
(1)△AEF是什么三角形?证明你的结论.
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
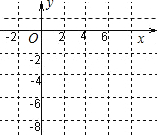
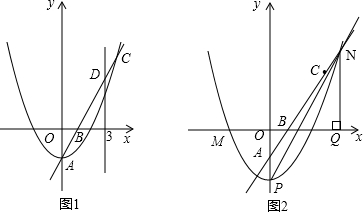
(3)如图(5),将矩形纸片ABCD沿EF折叠,使点A落在DC边上的点A′处,x轴垂直平分DA,直线EF的表达式为y=kx-k (k<0)
①问:EF与抛物线y=-
x2 有几个公共点?
②当EF与抛物线只有一个公共点时,设A′(x,y),求
的值.
第一步:先把矩形ABCD对折,折痕为MN,如图(1)所示;
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB′E,如图(2)所示;
第三步:沿EB′线折叠得折痕EF,如图(3)所示;利用展开图(4)所示.

探究:
(1)△AEF是什么三角形?证明你的结论.
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
(3)如图(5),将矩形纸片ABCD沿EF折叠,使点A落在DC边上的点A′处,x轴垂直平分DA,直线EF的表达式为y=kx-k (k<0)
①问:EF与抛物线y=-
| 1 |
| 8 |
②当EF与抛物线只有一个公共点时,设A′(x,y),求
| x |
| y |
(1)△AEF是等边三角形
证明:∵PE=PA,
B′P是RT△AB′E斜边上的中线
∴PA=B′P,
∴∠EAB′=∠PB′A,
又∵PN∥AD,
∴∠B′AD=∠PB′A,
又∵2∠EAB′+∠B′AD=90°,
∴∠EAB′=∠B′AD=30°,
易证∠AEF=60°,∴∠EAF=60°,
∴△AEF是等边三角形;
(2)不一定,
设矩形的长为a,宽为b,可知b≤
a时,一定能折出等边三角形,
当
a<b<a时,不能折出;
(3)①由
,
得x2+8kx-8k=0,△=(8k)2+32k=32k(2k+1),
∵k<0.
∴k<-
时,△>0,EF与抛物线有两个公共点.
当k=-
,△=0时,EF与抛物线有一个公共点.
当k>-
,△<0时,EF与抛物线没有公共点,
②EF与抛物线只有一个公共点时,k=-
,
EF的表达式为y=-
x+
,
EF与x轴、y轴的交点为M(1,0),E(0,
),
∵∠EMO=90°-∠OEM=∠EAA′,
∴RT△EMO∽RT△A′AD,
=
,
即
=
,
∴
=1.
证明:∵PE=PA,
B′P是RT△AB′E斜边上的中线
∴PA=B′P,
∴∠EAB′=∠PB′A,
又∵PN∥AD,
∴∠B′AD=∠PB′A,
又∵2∠EAB′+∠B′AD=90°,
∴∠EAB′=∠B′AD=30°,
易证∠AEF=60°,∴∠EAF=60°,
∴△AEF是等边三角形;
(2)不一定,
设矩形的长为a,宽为b,可知b≤
| ||
| 2 |
当
| ||
| 2 |
(3)①由
|
得x2+8kx-8k=0,△=(8k)2+32k=32k(2k+1),
∵k<0.
∴k<-
| 1 |
| 2 |
当k=-
| 1 |
| 2 |
当k>-
| 1 |
| 2 |
②EF与抛物线只有一个公共点时,k=-
| 1 |
| 2 |
EF的表达式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
EF与x轴、y轴的交点为M(1,0),E(0,
| 1 |
| 2 |
∵∠EMO=90°-∠OEM=∠EAA′,
∴RT△EMO∽RT△A′AD,
| OE |
| OM |
| DA/ |
| DA |
即
| ||
| 1 |
| x |
| 2y |
∴
| x |
| y |


练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
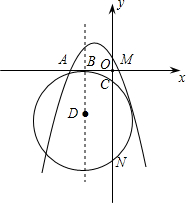

 O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.
O)的顶点C在直线AB上,以C为圆心,CA的长为半径作⊙C.