Question

有一座抛物线型拱桥，其水面宽AB为18米，拱顶O离水面AB的距离OM为8米，货船在水面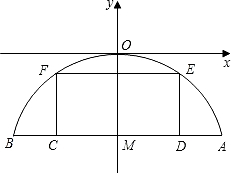上的部分的横断面是矩形CDEF，如图建立平面直角坐标系．
（1）求此抛物线的解析式；
（2）如果限定矩形的长CD为9米，那么矩形的高DE不能超过多少米，才能使船通过拱桥；
（3）若设EF=a，请将矩形CDEF的面积S用含a的代数式表示，并指出a的取值范围．

Answer 1

（1）y=-

8

81

x²（-9≤x≤9）（2分）

（2）∵CD=9
∴点E的横坐标为

9

2

，则点E的纵坐标为-

8

81

×(

9

2

)2=-2
∴点E的坐标为(

9

2

，-2)，
因此要使货船能通过拱桥，则货船最大高度不能超过8-2=6（米）（5分）

（3）由EF=a，则E点坐标为(

1

2

a，-

2

81

a2)，
此时ED=8-|-

2

81

a2|=8-

2

81

a2
∴S_矩形CDEF=EF•ED=8a-

2

81

a³（0＜a＜18）．（7分）