ĢāÄæÄŚČŻ
”¾ĢāÄæ”æij¹«½»³µĆæĢģµÄÖ§³ö·ŃÓĆĪŖ60 ŌŖ£¬ĆæĢģµÄ³Ė³µČĖŹż x£ØČĖ£©ÓėĆæĢģĄūČó£ØĄūČó £½Ę±æīŹÕČė £Ö§³ö·ŃÓĆ£©y£ØŌŖ£©µÄ±ä»Æ¹ŲĻµČēĻĀ±ķĖłŹ¾£ØĆæĪ»³ĖæĶµÄ³Ė³µĘ±¼Ū¹Ģ¶Ø²»±ä£©£ŗ
x£ØČĖ£© | ” | 200 | 250 | 300 | 350 | 400 | ” |
y£ØŌŖ£© | ” | £20 | £10 | 0 | 10 | 20 | ” |
øł¾Ż±ķøńÖŠµÄŹż¾Ż£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ŌŚÕāøö±ä»Æ¹ŲĻµÖŠ£¬×Ō±äĮæŹĒŹ²Ć“£æŅņ±äĮæŹĒŹ²Ć“£æ
£Ø2£©ČōŅŖ²»æ÷±¾£¬øĆ¹«½»³µĆæĢģ³ĖæĶČĖŹżÖĮÉŁ“ļµ½¶ąÉŁ£æ
£Ø3£©ĒėÄćÅŠ¶ĻŅ»Ģģ³ĖæĶČĖŹżĪŖ 5 00ČĖŹ±£¬ĄūČóŹĒ¶ąÉŁ£æ
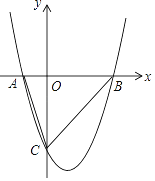
£Ø4£© ŹŌŠ“³öøĆ¹«½»³µĆæĢģĄūČó y£ØŌŖ£©ÓėĆæĢģ³Ė³µČĖŹżx £ØČĖ£©µÄ¹ŲĻµŹ½£®
”¾“š°ø”æ£Ø1£©ĆæĢģµÄ³Ė³µČĖŹż£¬ĆæĢģµÄĄūČ󣻣Ø3£©300£»£Ø3£©40£»£Ø4£©y=![]() x-60£®
x-60£®
”¾½āĪö”æ
£Ø1£©øł¾Ż×Ō±äĮ攢Ņņ±äĮæµÄ¶ØŅ壬½įŗĻĢāŅā¼“æɽā“š£»£Ø2£©¹Ū²ģ±ķøńÖŠµÄŹż¾Ż¼“æɽā“š£»£Ø3£©¹Ū²ģ±ķøńÖŠµÄŹż¾ŻæÉÖŖ£¬³Ė³µČĖŹżĆæŌö¼Ó50ČĖ£¬ĆæĢģµÄĄūČóŌö¼Ó10ŌŖ£¬ÓÉ“Ė¼“æɽā“š£»£Ø4£©ÉčĆæĪ»³ĖæĶµÄ¹«½»Ę±¼ŪĪŖaŌŖ£¬øł¾ŻĢāŅāµĆy=ax-60£¬ŌŚ°Ńx=200£¬y=-20“śČėy=ax-60£¬ĒóµĆaµÄÖµ£¬ÓÉ“Ė¼“æÉĒóµĆøĆ¹«½»³µĆæĢģĄūČóy£ØŌŖ£©ÓėĆæĢģ³Ė³µČĖŹżx £ØČĖ£©µÄ¹ŲĻµŹ½£®
£Ø1£©ŌŚÕāøö±ä»Æ¹ż³ĢÖŠ£¬ĆæĢģµÄ³Ė³µČĖŹżŹĒ×Ō±äĮ棬ĆæĢģµÄĄūČóŹĒŅņ±äĮ棻
£Ø2£©øł¾Ż±ķøńæÉµĆ£ŗµ±ĆæĢģ³Ė³µČĖŹżÖĮÉŁ“ļµ½300ČĖŹ±£¬øĆ¹«½»³µ²Å²»»įæ÷Ėš£»
£Ø3£©¹Ū²ģ±ķøńÖŠµÄŹż¾ŻæÉÖŖ£¬³Ė³µČĖŹżĆæŌö¼Ó50ČĖ£¬ĆæĢģµÄĄūČóŌö¼Ó10ŌŖ£¬
”ąµ±ĆæĢģµÄ³ĖæĶČĖŹżĪŖ 5 00ČĖŹ±£¬ĄūČóĪŖ40ŌŖ.
£Ø4£©ÉčĆæĪ»³ĖæĶµÄ¹«½»Ę±¼ŪĪŖaŌŖ£¬
øł¾ŻĢāŅāµĆ£ŗy=ax-60£¬
°Ńx=200£¬y=-20“śČėy=ax-60£¬
µĆ£ŗ200a-60=-20
½āµĆ£ŗa=![]() £¬
£¬
”ąy=![]() x-60£®
x-60£®

”¾ĢāÄæ”æijŠ£Ęß(1)°ąŃ§ÉśĪŖĮĖ½āijŠ”Ēų¼ŅĶ„ŌĀ¾łÓĆĖ®Ēéæö,Ė껜µ÷²éĮĖøĆŠ”Ēų²æ·Ö¼ŅĶ„,²¢½«µ÷²éŹż¾Ż½ųŠŠČēĻĀÕūĄķ,ŅŃÖŖøĆŠ”ĒųÓĆĖ®Įæ²»³¬¹ż![]() µÄ¼ŅĶ„Õ¼±»µ÷²é¼ŅĶ„×ÜŹżµÄ°Ł·Ö±ČĪŖ12%£¬Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
µÄ¼ŅĶ„Õ¼±»µ÷²é¼ŅĶ„×ÜŹżµÄ°Ł·Ö±ČĪŖ12%£¬Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
¼¶±š |
|
|
|
|
|
|
ŌĀ¾łÓĆĖ®Įæ |
|
|
|
|
|
|
ʵŹż£Ø»§£© | 6 | 12 |
| 10 | 4 | 2 |
£Ø1£©±¾“Īµ÷²é²ÉÓƵķ½Ź½ŹĒ £ØĢī”°Ęղ锱»ņ”°³éŃłµ÷²é”±£©£¬Ńł±¾ČŻĮæŹĒ £»
£Ø2£©²¹Č«ĘµĀŹ·Ö²¼Ö±·½Ķ¼£»

£Ø3£©Čō½«µ÷²éŹż¾Ż»ęÖĘ³ÉÉČŠĪĶ³¼ĘĶ¼£¬ŌņŌĀ¾łÓĆĖ®Įæ”°![]() ”±µÄŌ²ŠÄ½Ē¶ČŹżŹĒ .
”±µÄŌ²ŠÄ½Ē¶ČŹżŹĒ .