题目内容
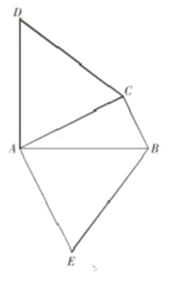
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
【答案】(1)详见解析;(2)详见解析;
【解析】
(1)利用垂直证明∠DAC=∠EAB,即可证明全等;
(2)①根据AE=AC,∠ACB=90°,可得∠ACE=∠BCE=45°;
②延长DC交EB于F,先求出∠D=∠ABE,得到∠D+∠BAE+∠AEB=180°,再根据∠D+∠BAD+∠AEB+∠BAE+∠F=360°,求出∠F即可.
(1)∵DA⊥AB,EA⊥AC
∴∠DAB=∠CAE=90°
∴∠DAC+∠CAB=∠BAE+∠CAB
∴∠DAC=∠EAB
∵AD=AB,AE=AC
∴△ACD≌△AEB;
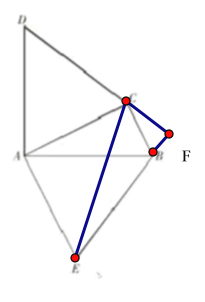
(2)①连接CE,∵DC⊥EB
∵EA⊥AC,AE=AC
∴∠ACE=∠CEA=45°
∵∠ACB=90°
∴∠BCE=45°=∠ACE
∴EC平分∠ACB
②延长DC交EB于F,
∵△ACD≌△AEB
∴∠D=∠ABE
∵∠ABE+∠BAE+∠AEB=180°
∴∠D+∠BAE+∠AEB=180°
∵∠D+∠BAD+∠AEB+∠BAE+∠F=360°
∴∠D+∠BAE+∠AEB+∠BAD+∠F=360°
∴180°+90°+∠F=360°
∴∠F=90°
∴DC⊥EB

 优学名师名题系列答案
优学名师名题系列答案【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
【题目】某校举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数 | 人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根据以上信息解决下列问题:
(1)在统计表中,![]() __________,
__________,![]() __________,并补全直方图;
__________,并补全直方图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是__________度;
组”所对应的圆心角的度数是__________度;
(3)若该校共有![]() 名学生,如果听写正确的个数少于
名学生,如果听写正确的个数少于![]() 个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.