题目内容
【题目】已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点(A在B的左边),与y轴交于点C.
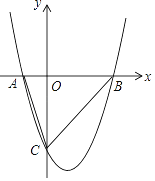
(1)求出点A、B、C的坐标.
(2)求S△ABC
(3)在抛物线上(除点C外),是否存在点N,使得S△NAB=S△ABC , 若存在,求出点N的坐标,若不 存在,请说明理由.
【答案】(1)A(﹣1,0)、B(3,0);(2)6;(3)存在,点N的坐标(1+ ![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3)
,3)或(2,﹣3)
【解析】试题分析:
(1)在解析式![]() 中,由
中,由![]() ,求得
,求得![]() 的对应值可得点C的坐标;由
的对应值可得点C的坐标;由![]() ,求得对应的
,求得对应的![]() 的值可得点A、B的坐标;
的值可得点A、B的坐标;
(2)根据(1)中所求点A、B、C坐标可求得△ABC的面积;
(3)设点N的纵坐标为![]() ,则由S△NAB=S△ABC可知
,则由S△NAB=S△ABC可知![]() 或
或![]() ,由点N在抛物线
,由点N在抛物线![]() 上,可得
上,可得![]() 或
或![]() ,解方程即可求得点N的横坐标,从而得到点N的坐标.
,解方程即可求得点N的横坐标,从而得到点N的坐标.
试题解析:
(1)在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴点C的坐标为:(0,﹣3),
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
∴点A的坐标为:(﹣1,0)、点B的坐标为:(3,0);
(2)∵点A的坐标为:(﹣1,0)、点B的坐标为:(3,0),
∴AB=3+1=4,
∵点C的坐标为:(0,﹣3),
∴OC=3,
∴S△ABC= ![]() ABOC=
ABOC=![]() ×4×3=6;
×4×3=6;
(3)存在点N,使S△NAB=S△ABC,
设点N的纵坐标为![]() ,
,
∵S△NAB=S△ABC,OC=3,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
解得:![]() 或
或![]() ,
,
∵点N不与点C重合,
∴点N的坐标为:(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)或(2,﹣3).
,3)或(2,﹣3).

【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次 | 第2次 | 第3次 | |
提现金额(元) | A | b |
|
手续费(元) | 0 | 0.4 | 3.4 |
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.
【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.