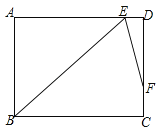
题目内容
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 在
在![]() 上,且
上,且![]() ,设
,设![]() .
.

(1)当![]() 时,如图2,求
时,如图2,求![]() 的长;
的长;

(2)设![]() ,求
,求![]() 关于
关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(3)若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的长.
的长.
【答案】(1)![]() =
=![]() (2)y=
(2)y=![]() x-8(
x-8(![]() ≤x≤
≤x≤![]() )(3)4
)(3)4![]()
【解析】
(1)先根据菱形的边长和对角线的长得到∠ABO =30°,再根据![]() ,求出AP的长,故可得到DP的长;
,求出AP的长,故可得到DP的长;
(2)作HP⊥AB,根据AP=PQ,得到AH=QH=![]() ,BH=8-
,BH=8-![]() ,BP=BD-DP=
,BP=BD-DP=![]() -x,再根据(1)可得HP=
-x,再根据(1)可得HP=![]() -
-![]() x,在Rt△BPH中,BP2=HB2+HP2,化简即可求解,再求出x的取值范围;
x,在Rt△BPH中,BP2=HB2+HP2,化简即可求解,再求出x的取值范围;
(3)根据题意作图,由等腰三角形的性质可得△AQP是等边三角形,故可得到DP的长.
(1)∵![]() ,
,![]() ,
,
∴BO=![]() =4
=4![]() ,AC⊥BD
,AC⊥BD
故AO=![]() =4=
=4=![]()
∴∠ABO =30°=∠ADO
∵![]()
∴∠APB =90°-∠ABO =60°
故∠PAD=∠APB -∠ADO =30°
即∠PAD=∠ADO
∴DP=AP
设AP=x,则BP=2x,
在Rt△ABP中,BP2=AB2+AP2
即(2x)2=82+x2
解得x=![]()
故![]() =
=![]() ;
;
(2)作HP⊥AB,∵AP=PQ
∴AH=QH=![]()
∴BH=BQ+QH=(8-y)+![]() =8-
=8-![]() ,
,
BP=BD-DP=![]() -x,
-x,
由(1)可得HP=![]() =
=![]() -
-![]() x
x
在Rt△BPH中,BP2=HB2+HP2
即(![]() -x)2=(8-
-x)2=(8-![]() )2+(
)2+(![]() -
-![]() x)2
x)2
∵![]() -x>0,8-
-x>0,8-![]() >0,
>0,![]() -
-![]() x>0
x>0
∴化简得y=![]() x-8
x-8
∵0≤![]() x-8≤8
x-8≤8
∴x的取值范围为![]() ≤x≤
≤x≤![]()
∴![]() 关于
关于![]() 的函数关系式是y=
的函数关系式是y=![]() x-8(
x-8(![]() ≤x≤
≤x≤![]() );
);
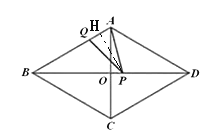
(3)如图,若![]() 是以
是以![]() 为腰的等腰三角形,
为腰的等腰三角形,
则∠QPB=∠QBP=30°,
∴∠AQP=∠QPB+∠QBP=60°
∵∠BAP=90°-∠QBP=60°,
∴△APQ是等边三角形,∠APQ=60°
∴∠QPB +∠APQ=90°,
则AP⊥BP,故O点与P点重合,
∴PD=DO=![]() =4
=4![]() .
.


 优学名师名题系列答案
优学名师名题系列答案【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.