题目内容
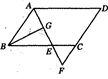
(10分)如图,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.

小题1:(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
小题2:(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图,连接AE和GC. 你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.

小题1:(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
小题2:(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图,连接AE和GC. 你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.

小题1:(1) AE⊥CE,由△ADE≌△CDG可证;
小题2:(2)(1)的结论仍然成立,证明方法同(1)
分析:
(1)观察图形,AE、CG的数量关系可能是相等,下面着手证明.由于四边形ABCD、DEFG都是正方形,由SAS易证得△ADE≌△CDG,则AE=GC;
(2)(1)中的结论仍然成立,参照(1)题的解题方法,可由SAS证得△ADE≌△CDG,得AE=GC;
解答:

(1)结论为:AE=GC。理由如下:
在正方形ABCD与正方形DEFG中,
AD=DC,∠ADE=∠CDG=90°,DE=DG,
∴△ADE≌△CDG,
∴AE=GC。
(2)(1)中的结论仍然成立,理由如下:
在正方形ABCD和正方形DEFG中,
AD=DC,DE=DG,∠ADC=∠EDG=90°,
∴∠1=∠2=90°-∠3;
∴△ADE≌△CDG,
∴AE=GC。
点评:本题主要考查旋转的性质以及全等三角形的判定和性质。需要注意的是:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
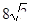 B.
B. 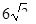 C.
C. 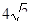 D.
D. 



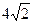 cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。
 A1BCD1,若
A1BCD1,若
 ,则△CEF的周长为
,则△CEF的周长为