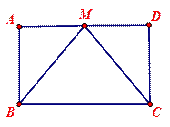
题目内容
把正方形ABCD对折,得到折痕MN(如图①),展开后把正方形ABCD沿CE折叠,使点B落在MN上的点B’处,连结B’D(如图②)。
试求∠BCB’及∠ADB’的度数。(4分+4分=8分。)

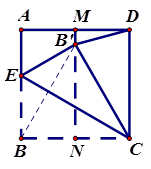
图① 图②
试求∠BCB’及∠ADB’的度数。(4分+4分=8分。)


图① 图②
∠BCB’=60° ∠ADB’=15°
利用翻折变换的性质得出以及垂直平分线的性质得出BC=B′C,BB′=B′C,进而得出△B′BC是等边三角形,再利用等腰三角形的性质求出∠ADB′的度数即可.
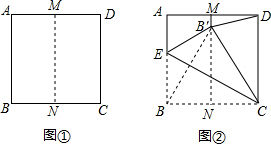
解:∵点B落在MN上的点B′处,把正方形ABCD对折,得到折痕MN,
∴BC=B′C,BB′=B′C,
∴BC=BB′=B′C,
∴△B′BC是等边三角形,
∴∠BCB′=60°,
∴∠B′CD=30°,
∵DC=B′C,
∴∠CB′D=∠CDB′,
∴∠CB′D=∠CDB′=1/2×150°=75°,
∴∠ADB′=15°.

练习册系列答案
相关题目

 。
。


 ABCD的两条对角线线交于O,且
ABCD的两条对角线线交于O,且 。
。