题目内容
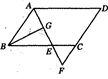
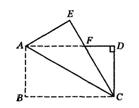
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E, 交DC的延长线于点F,BG⊥AE,垂足为G,BG=4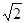 ,则△CEF的周长为
,则△CEF的周长为
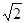 ,则△CEF的周长为
,则△CEF的周长为
| A.8 | B.9.5 | C.10 | D.5 |
A
解:∵在?ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DF,
∠BAF=∠F,
∴∠F=∠DAF,
∴△ADF是等腰三角形,AD=DF=9;
∵AB=CD=6,
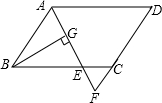
∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG=4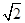 ,可得:AG=2,
,可得:AG=2,
又∵BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵?ABCD,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故答案为8.
∴∠BAF=∠DAF,
∵AB∥DF,
∠BAF=∠F,
∴∠F=∠DAF,
∴△ADF是等腰三角形,AD=DF=9;
∵AB=CD=6,

∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG=4
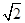 ,可得:AG=2,
,可得:AG=2,又∵BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵?ABCD,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故答案为8.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目


 ABCD的两条对角线线交于O,且
ABCD的两条对角线线交于O,且 。
。

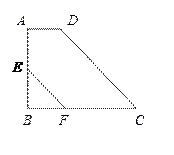
 的两条对角线交于点
的两条对角线交于点 ,图中面积相等的三角形共
,图中面积相等的三角形共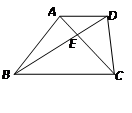
 中,
中, 是
是 上的一个动点(不与
上的一个动点(不与 重合),连接
重合),连接 交对角线
交对角线 于
于 ,连接
,连接 .
.
 ;
; ,试问
,试问 的面积等于菱形
的面积等于菱形 ?为什么?
?为什么?
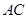 为正方形
为正方形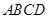 的对角线,
的对角线,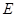 为
为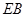 ,
,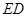 ,当
,当 时,
时,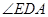 的度数为( )
的度数为( )