题目内容
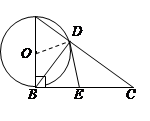
如图,已知Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连结BD。(12分)

(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连结DE,求证:ED与⊙O相切。

(1)若AD=3,BD=4,求边BC的长;
(2)取BC的中点E,连结DE,求证:ED与⊙O相切。
(1)解:∵AB是⊙O的直径 ∴∠ADB=90° ………………1分
在Rt△ABD中,AD=3,BD=4
∴AB=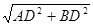 =
=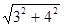 =5 ………………2分
=5 ………………2分
∵∠BAD=∠CAB ∠ADB=∠ABC=90°
∴△ADB∽△ABC ………………4分
∴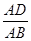 =
=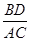 即
即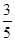 =
=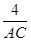
 ∴AC=
∴AC=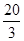 ………………6分 (2)证明:连结OD
………………6分 (2)证明:连结OD
∵AB是⊙O的直径
∴∠ADB=90° ∴∠BDC=90°
∴△BDC是直角三角形 …………7分
又E是BC中点
∴DE=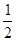 BC=BE ………………8分
BC=BE ………………8分
∴∠DBE=∠BDE
∵OB=OD
∴∠OBD=∠ODB ………………10分
∴∠OBD+∠DBE=∠ODB+∠BDE
即∠ODE=∠ABC=90°
又∵OD是⊙O的半径
∴ED与⊙O相切 ………………12分
在Rt△ABD中,AD=3,BD=4
∴AB=
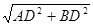 =
=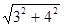 =5 ………………2分
=5 ………………2分∵∠BAD=∠CAB ∠ADB=∠ABC=90°
∴△ADB∽△ABC ………………4分
∴
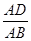 =
=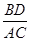 即
即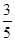 =
=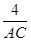
|
 ∴AC=
∴AC=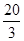 ………………6分 (2)证明:连结OD
………………6分 (2)证明:连结OD∵AB是⊙O的直径
∴∠ADB=90° ∴∠BDC=90°
∴△BDC是直角三角形 …………7分
又E是BC中点
∴DE=
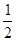 BC=BE ………………8分
BC=BE ………………8分∴∠DBE=∠BDE
∵OB=OD
∴∠OBD=∠ODB ………………10分
∴∠OBD+∠DBE=∠ODB+∠BDE
即∠ODE=∠ABC=90°
又∵OD是⊙O的半径
∴ED与⊙O相切 ………………12分
略

练习册系列答案
相关题目
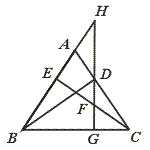
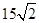 cm,∠ACB=90°现要沿AB边向上依次截取宽度均为2cm的长方形纸条,如图所示.已知截得的长方形纸片中有一块是正方形,则这块正方形纸片是( )
cm,∠ACB=90°现要沿AB边向上依次截取宽度均为2cm的长方形纸条,如图所示.已知截得的长方形纸片中有一块是正方形,则这块正方形纸片是( )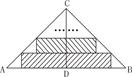
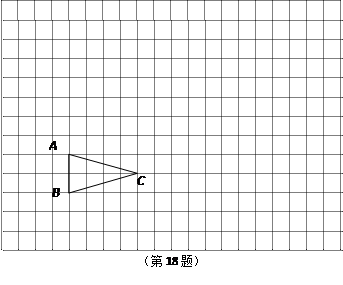


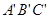 是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
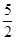 ,3),则A′的坐标为 ;
,3),则A′的坐标为 ;
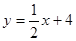 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.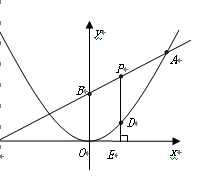
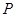 为线段
为线段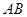 上的一个动点(点
上的一个动点(点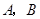 不重合),过
不重合),过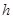 ,点
,点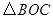 相似?若存在,请求出
相似?若存在,请求出