题目内容
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
【答案】(1)4种,甲47,乙53;甲48,乙52;甲49,乙51;甲50,乙50(2)甲47,乙53利润最大,最大利润1106元
【解析】
(1)利用购书款不高于1118元,预计这100本图书全部售完的利润不低于1100元,结合表格中数据得出不等式组,求出即可;
(2)设利润为W,根据题意得W=10x+12(100-x)=-2x+1200,W随x的增大而减小,故购进甲种书:47种,乙种书:53本利润最大,代入求出即可;
解:(1)设购进甲种图书x本,则购进乙书(100-x)本,根据题意得出:
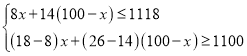
解得:47≤x≤50.
故有4种购书方案:甲47,乙53;甲48,乙52;甲49,乙51;甲50,乙50;
(2)设利润为W,根据题意得
W=10x+12(100-x)=-2x+1200,
根据一次函数的性质得,W随x的增大而减小,
故购进甲种书:47本,乙种书:53本,利润最大,
最大利润W=-2×47+1200=1106,
所以甲47,乙53利润最大,最大利润1106元.
故答案为:(1)4种,甲47,乙53;甲48,乙52;甲49,乙51;甲50,乙50(2)甲47,乙53利润最大,最大利润1106元

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目