题目内容
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,ED⊥AB于F,
(1)求证:△CDE是等腰三角形;
(2)若AB=4,![]() ,求证:△OBC≌△DCE.
,求证:△OBC≌△DCE.
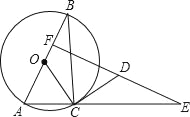
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析(1)由于AB是直径,那么∠ACB=90°,而∠ABC=30°,易求∠BAC=60°,结合OA=OC,易证△AOC是正三角形,于是∠OCD=60°,结合CD是切线,易求∠DCE=30°,在Rt△AEF中,易求∠E=30°,于是∠DCE=∠E,可证△CDE实等腰三角形;
(2)在Rt△ABC中,由于∠A=60°,AB=4,易求AC=AO=2,利用勾股定理可求BC=2![]() ,CE=AE-AC=2
,CE=AE-AC=2![]() ,那么BC=CE,而∠OBC=∠OCB=∠DCE=∠DEC=30°,从而可证△OBC≌△DCE.
,那么BC=CE,而∠OBC=∠OCB=∠DCE=∠DEC=30°,从而可证△OBC≌△DCE.
试题解析:证明:(1)∵AB为直径,
∴∠ACB=90°,
又∠ABC=30°,
∴∠BAC=60°,
又∵OA=OC,
∴△AOC是正三角形,
又∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠DCE=180°﹣60°﹣90°=30°,
又∵ED⊥AB于F,
∴∠DEC=90°﹣∠BAC=30°,
∴∠DCE=∠DEC,
故△CDE为等腰三角形;
(2)在Rt△ABC中,
∵AB=4,AC=AO=2,
∴![]() ,
,
而![]() ,
,
∴BC=CE,
又∵∠OBC=∠OCB=∠DCE=∠DEC=30°,
∴△OBC≌△DCE(ASA).

 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)