Question

【题目】已知数轴上有A，B，C三点，分别代表﹣36，﹣10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位/秒．

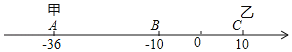
（1）问多少秒后，甲到A，B，C的距离和为60个单位？

（2）若乙的速度为6个单位/秒，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，问甲，乙在数轴上的哪个点相遇？

（3）在（1）（2）的条件下，当甲到A、B、C的距离和为60个单位时，甲调头返回．问甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．

Answer 1

【答案】（1）经过3s或10s后，甲到A，B，C的距离和为60个单位；（2）甲，乙在数轴上的点﹣17.6相遇；（3）甲从A向右运动3秒时返回，能在数轴上与乙相遇，相遇点表示的数为﹣56．

【解析】

（1）设x秒后甲到A，B，C三点的距离之和为60个单位，分甲应为于AB或BC之间两种情况讨论即可求解；
（2）可设x秒后甲与乙相遇，根据甲与乙的路程和为46，可列出方程求解即可；
（3）设y秒后甲到A，B，C三点的距离之和为60个单位，分甲应为于AB或BC之间两种情况讨论即可求解．

解：（1）设x秒后，甲到A，B，C的距离和为60个单位．

B点距A，C两点的距离为26+20＝46＜60，

A点距B、C两点的距离为26+46＝72＞60，

C点距A、B的距离为46+20＝66＞40，

故甲应位于AB或BC之间．

①AB之间时：4x+（26﹣4x）+（26﹣4x+20）＝60，x＝3；

②BC之间时：4x+（4x﹣26）+（46﹣4x）＝60，x＝10，

综上所述，经过3s或10s后，甲到A，B，C的距离和为60个单位；

（2）设ts后甲与乙相遇

4t+6t＝46，

解得：x＝4.6，

4×4.6＝18.4，﹣36+18.4＝﹣17.6

答：甲，乙在数轴上的点﹣17.6相遇；

（3）设y秒后甲到A，B，C三点的距离之和为60个单位，

①甲从A向右运动3秒时返回，此时甲、乙表示在数轴上为同一点，所表示的数相同．

甲表示的数为：﹣36+4×3﹣4y；乙表示的数为：10﹣6×3﹣6y，

依据题意得：﹣36+4×3﹣4y＝10﹣6×3﹣6y，

解得：y＝8，

相遇点表示的数为：﹣36+4×3﹣4y＝﹣56（或：10﹣6×3﹣6y＝﹣56），

②甲从A向右运动10秒时返回，设y秒后与乙相遇．

甲表示的数为：﹣36+4×10﹣4y；乙表示的数为：10﹣6×10﹣6y，

依据题意得：﹣36+4×10﹣4y＝10﹣6×10﹣6y，

解得：y＝﹣27（不合题意舍去），

即甲从A向右运动3秒时返回，能在数轴上与乙相遇，相遇点表示的数为﹣56．