Question

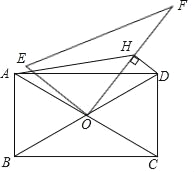
【题目】如图，在矩形ABCD中，AB＝4，BC＝4，对角线AC、BD相交于点O，现将一个直角三角板OEF的直角顶点与O重合，再绕着O点转动三角板，并过点D作DH⊥OF于点H，连接AH．在转动的过程中，AH的最小值为_____．

Answer 1

【答案】2﹣2

【解析】

取OD的中点G，过G作GP⊥AD于P，连接HG，AG，依据∠ADB=30°，可得PGDG=1，依据∠DHO=90°，可得点H在以OD为直径的⊙G上，再根据AH+HG≥AG，即可得到当点A，H，G三点共线，且点H在线段AG上时，AH最短，根据勾股定理求得AG的长，即可得出AH的最小值．

如图，取OD的中点G，过G作GP⊥AD于P，连接HG，AG．

∵AB=4，BC=4AD，∴BD8，∴BD=2AB，DO=4，HG=2，∴∠ADB=30°，∴PGDG=1，∴PD，AP=3．

∵DH⊥OF，∴∠DHO=90°，∴点H在以OD为直径的⊙G上．

∵AH+HG≥AG，∴当点A，H，G三点共线，且点H在线段AG上时，AH最短，此时，Rt△APG中，AG，∴AH=AG﹣HG=22，即AH的最小值为22．

故答案为：22．