题目内容
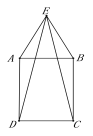
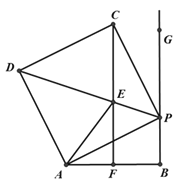
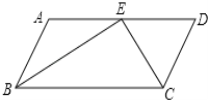
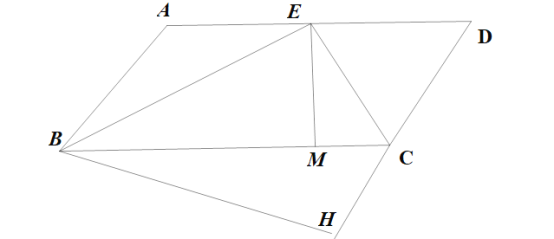
【题目】如图,在□ABCD中,∠ABC和∠BCD的平分线交边AD于点E,且BE=12,CE=5,则点AB与CD之间的距离是____
【答案】![]()
【解析】
根据平行四边形的性质可证明△BEC是直角三角形,利用勾股定理可求出BC的长,利用角平分线的性质以及平行线的性质得出∠ABE=∠AEB,∠DEC=∠DCE,进而利用平行四边形对边相等进而得出答案,最后根据平行四边形的面积求出AB与CD之间的距离.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的角平分线的交点E落在AD边上,
∴∠EBC+∠ECB=![]() ×180°=90°,
×180°=90°,
∴∠BEC=90°,
∵BE=12,CE=5,
∴BC=![]() =13
=13
作EM⊥BC于M,
则EM=![]() =
=![]()
∴点A到BC的距离是![]()
∵AD∥BC, ∠ABC和∠BCD的平分线交边AD于点E,
∴AE=AB,ED=CD,即AB=CD=![]() AD=
AD=![]()
延长CD,过B点作BH⊥CD于H,即BH就是AB到CD的距离。
∵S平行四边形ABCD=EM×BC=13×![]() =
=![]() ;
;
∴S平行四边形ABCD=CD×BH=![]() ×BH=
×BH=![]()
∴BH=![]()

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)