��Ŀ����
����Ŀ����ͼ��ʾ��������ABCD�У���E��F��G�ֱ��DZ�AD��AB��BC���е㣬����EP��FG��
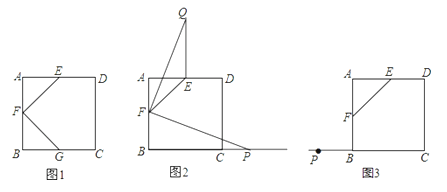
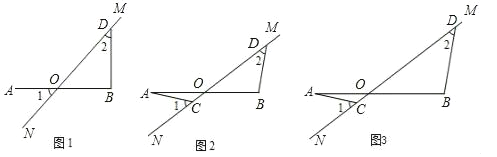
��1����ͼ1��ֱ��д��EF��FG�Ĺ�ϵ____________��
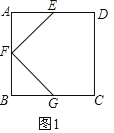
��2����ͼ2������PΪBC�ӳ�����һ���㣬����FP�����߶�FP�Ե�FΪ��ת���ģ���ʱ����ת90�㣬�õ��߶�FH������EH��
����֤����FFE�ա�PFG����ֱ��д��EF��EH��BP����֮��Ĺ�ϵ��
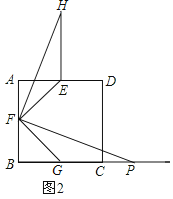
��3����ͼ3������PΪCB�ӳ����ϵ�һ���㣬����FP������(2)�е���������ͼ(3)�в�ȫͼ�Σ���ֱ��д��EF��EH��BP����֮��Ĺ�ϵ��
���𰸡���1��EF��FG��EF=FG����2�������������3����ȫͼ����ͼ3��ʾ��![]() EF+BP=EH��
EF+BP=EH��
��������
��1�������߶��е�Ķ������AE=AF=BF=BG���ó���AFE=��AEF=��BFG=��BGF=45�㣬�����EFG�Ķ���������SAS��֤����AEF����BFGȫ�ȣ��ó�EF=FG�����ɵó������
��2��������ת�����ʵó���PFH=90����FP=FH��֤����GFP=��EFH����SAS���ɵó���HFE�ա�PFG��
����ȫ�������ε����ʵó�EH=PG���ɵ���ֱ�������ε����ʵó�EF=![]() AF=
AF=![]() BG�����BG=
BG�����BG=![]() EF������BG+GP=BP�����ɵó����ۣ�
EF������BG+GP=BP�����ɵó����ۣ�
��3��������������ͼ�Σ�Ȼ��ͬ��2����˼·��⼴�ɣ�
�⣺��1����ͼ1��ʾ��
�ߵ�E��F��G�ֱ��DZ�AD��AB��BC���е㣬
��AE=AF=BF=BG��
���ı���ABCD�������Σ�
���AFE=��AEF=��BFG=��BGF=45����
���EFG=180��-��AFE-��BFG=180��-45��-45��=90����
��EF��FG��
�ڡ�AEF�͡�BFG�У�
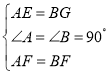 ��
��
���AEF�ա�BFG��SAS����
��EF=FG��
�ʴ�Ϊ��EF��FG��EF=FG��
��2����ͼ2��ʾ��
��֤�����ɣ�1���ã���EFG=90����EF=FG��
�߽��߶�FP�Ե�FΪ��ת���ģ���ʱ����ת90�����õ��߶�FH��
���PFH=90����FP=FH��
�ߡ�GFP+��PFE=90������PFE+��EFH=90����
���GFP=��EFH��
�ڡ�HFE�͡�PFG�У�
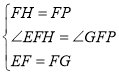 ��
��
���HFE�ա�PFG��SAS����
�ڽ⣺�ɢٵã���HFE�ա�PFG����EH=PG��
��AE=AF=BF=BG����A=��B=90����
��EF=![]() AF=
AF=![]() BG��
BG��
��BG=![]() EF��
EF��
��BG+GP=BP��
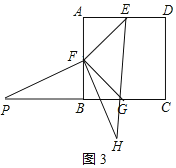
��![]() EF+EH=BP��
EF+EH=BP��
��3���⣺��ȫͼ����ͼ3��ʾ��![]() EF+BP=EH���������£�
EF+BP=EH���������£�
�ɣ�1���ã���EFG=90����EF=FG��
�߽��߶�FP�Ե�FΪ��ת���ģ���ʱ����ת90�����õ��߶�FH��
���PFH=90����FP=FH��
�ߡ�EFG+��GFH=��EFH����PFH+��GFH=GFP��
���GFP=��EFH��
�ڡ�HFE�͡�PFG�У�
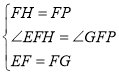 ��
��
���HFE�ա�PFG��SAS����
��EH=PG��
��AE=AF=BF=BG����A=��ABC=90����
��EF=![]() AF=
AF=![]() BG��
BG��
��BG=![]() EF��
EF��
��BG+BP=PG��
��![]() EF+BP=EH��
EF+BP=EH��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij����������ס�������ͼ�鹲100������������1118Ԫ��Ԥ��100��ͼ��ȫ�������������1100Ԫ������ͼ��Ľ��ۡ��ۼ������ʾ��
����ͼ�� | ����ͼ�� | |
���ۣ�Ԫ/���� | 8 | 14 |
�ۼۣ�Ԫ/���� | 18 | 26 |
��ش��������⣺
��1������ж����ֽ��鷽����
��2��������ͼ��ȫ���۳��������£���1���е����ַ������������������Ƕ��٣�����������ѧ��һ�κ���֪ʶ�������