题目内容
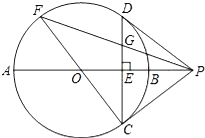
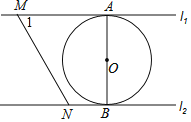
【题目】如图,直线11∥l2,⊙O与11和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.
(1)当MN与⊙O相切时,求AM的长;
(2)当∠MON为多少度时,MN与⊙O相切,并给出证明.
【答案】(1)AM的长为![]() 或
或![]() ;(2)当∠MON=90°时,MN与⊙O相切;证明见解析.
;(2)当∠MON=90°时,MN与⊙O相切;证明见解析.
【解析】
(1)连结OM,ON,当MN在AB左侧时,根据切线长定理得∠AMO![]() ∠AMN=30°.在Rt△AMO中,利用正切的定义可计算出AM
∠AMN=30°.在Rt△AMO中,利用正切的定义可计算出AM![]() .当MN在AB右侧时,同理可得:AM'
.当MN在AB右侧时,同理可得:AM'![]() ;
;
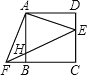
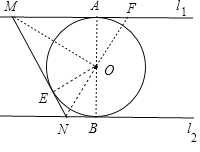
(2)当∠MON=90°时,MN与⊙O相切,作OE⊥MN于E,延长NO交l1于F,易证得Rt△OAF≌Rt△OBN,则OF=ON,于是可判断MO垂直平分NF,所以OM平分∠NMF,根据角平分线的性质得OE=OA,然后根据切线的判定定理得到MN为⊙O的切线.
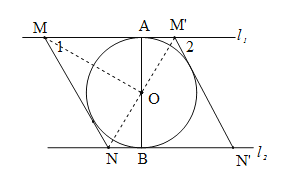
(1)当MN与⊙O相切,如图,连结OM,ON,分两种情况讨论:
①当MN在AB左侧时,∠AMO![]() ∠AMN
∠AMN![]() 60°=30°.在Rt△AMO中,tan∠AMO
60°=30°.在Rt△AMO中,tan∠AMO![]() ,即AM
,即AM![]() ;
;
②当MN在AB右侧时,∠AM'O![]() ∠AM'N
∠AM'N![]() (180°-60°)=60°.在Rt△AM'O中,tan∠AM'O
(180°-60°)=60°.在Rt△AM'O中,tan∠AM'O![]() ,即AM'
,即AM'![]() .
.
综上所述:AM的长为![]() 或
或![]() ;
;
(2)当∠MON=90°时,MN与⊙O相切.证明如下:
作OE⊥MN于E,延长NO交l1于F,如图,∵⊙O与11和l2分别相切于点A和点B,∴∠OAF=∠OBN=90°.
∵直线11∥l2,∴A、O、B共线.
在△OAF和△OBN中,∵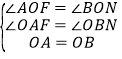 ,∴△OAF≌△OBN(AAS),∴OF=ON,∴MO垂直平分NF,∴OM平分∠NMF,∴OE=OA,∴MN为⊙O的切线.
,∴△OAF≌△OBN(AAS),∴OF=ON,∴MO垂直平分NF,∴OM平分∠NMF,∴OE=OA,∴MN为⊙O的切线.

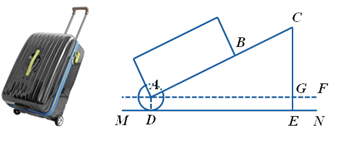
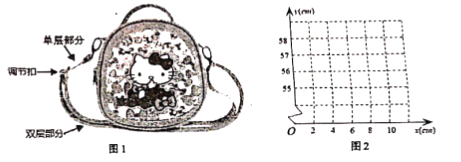
【题目】如图1是某品牌的一款学生斜持包,其挎带由单层部分、双层部分和调节扣组成.设单层部分的长度为xcm,双层部分的长度为ycm,经测景,得到如下数据:
x(cm) | 0 | 4 | 6 | 8 | 10 | … | 120 |
y(cm) | M | 58 | 57 | 56 | 55 | … | n |
(1)如图2,在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用平滑曲线连接,并根据图象猜想求出该函数的解析式;
(2)若小花要购买一个持带长为125cm的斜挎包,该款式的斜挎包是否满足小花的需求?请说明理由,(挎带的总长度=单层部分长度+双层部分长度,其中调节扣的长度忽略不计)