题目内容
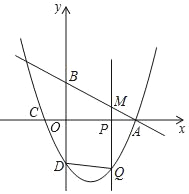
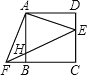
【题目】如图，△ADE绕正方形ABCD的顶点A顺时针旋转90°，得△ABF，连接EF交AB于H，则下列结论: ①AE⊥AF；②EF：AF=
：1；③AF2=FHFE；④FB：FC=HB：EC．正确的是___．
【答案】①②④．
【解析】
由旋转性质得到△AFB≌△AED，再根据相似三角对应边的比等于相似比，即可分别求得各选项正确与否．
由题意知，△AFB≌△AED，∴AF=AE，∠FAB=∠EAD，∠FAB+∠BAE=∠EAD+∠BAE=∠BAD=90°，∴AE⊥AF，故选项①正确；
∴△AEF是等腰直角三角形，有EF：AF
：1，故选项②正确；
∵△AEF与△AHF不相似，∴AF2=FHFE不正确．故选项③错误．
∵HB∥EC，∴△FBH∽△FCE，∴FB：FC=HB：EC，故选项④正确．
故选①②④．
【题目】水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数，并对数据进行整理、描述和分析。
下面给出了部分信息：（说明：45 个以下为产量不合格，45 个及以上为产量合格，其中 45～65 个为产量良好，65～85 个为产量优秀）
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x＜35，35≤x＜45，45≤x＜55，55≤x＜65，65≤x＜75，75≤x＜85):
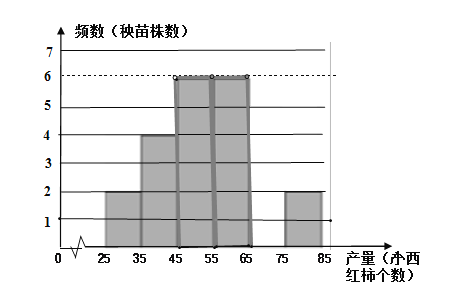
b.乙组数据在产量良好（45≤x＜65）这两组的具体数据为： 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示：
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
（1）补全乙的频数分布直方图.
（2）写出表中
的值．
（3）根据样本情况，估计乙大棚产量良好及以上的秧苗数为 株．
（4）根据抽样调查情况，可以推断出 大棚的小西红柿秧苗品种更适应市场需求，写出理由．（至少从两个不同的角度说明推断的合理性）．
