题目内容
【题目】甲、乙两车分别从相距480km的A、B两地相向而行，乙车比甲车先出发1小时，并以各自的速度匀速行驶，途径C地，甲车到达C地停留1小时，因有事按原路原速返回A地．乙车从B地直达A地，两车同时到达A地．甲、乙两车距各自出发地的路程y（千米）与甲车出发所用的时间x（小时）的关系如图，结合图象信息解答下列问题：
（1）乙车的速度是 千米/时，t＝ 小时；
（2）求甲车距它出发地的路程y与它出发的时间x的函数关系式，并写出自变量的取值范围；
（3）直接写出乙车出发多长时间两车相距120千米．
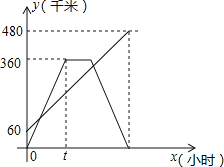
【答案】(1)60，3；
(2)①y=120t(0≤t≤3);②y=120(3＜t≤4);③y=-120t+840(4＜t≤7);
【解析】试题分析：（1）首先根据图示，可得乙车的速度是60千米/时，然后根据路程÷速度=时间，用两地之间的距离除以乙车的速度，求出乙车到达A地用的时间是多少；最后根据路程÷时间=速度，用两地之间的距离除以甲车往返AC两地用的时间，求出甲车的速度，再用360除以甲车的速度，求出t的值是多少即可．
（2）根据题意，分3种情况：①当0≤x≤3时；②当3＜x≤4时；③4＜x≤7时；分类讨论，求出甲车距它出发地的路程y与它出发的时间x的函数关系式，并写出自变量的取值范围即可．
（3）根据题意，分3种情况：①甲乙两车相遇之前相距120千米；②当甲车停留在C地时；③两车都朝A地行驶时；然后根据路程÷速度=时间，分类讨论，求出乙车出发多长时间两车相距120千米即可．
试题解析：（1）根据图示，可得
乙车的速度是60千米/时，
甲车的速度=720÷6=120（千米/小时）
∴t=360÷120=3（小时）．
（2）①当0≤x≤3时，设y=k1x，
把（3，360）代入，可得
3k1=360，
解得k1=120，
∴y=120x（0≤x≤3）．
②当3＜x≤4时，y=360．
③4＜x≤7时，设y=k2x+b，
把（4，360）和（7，0）代入，可得
，解得
∴y=﹣120x+840（4＜x≤7）．
（3）①÷+1=300÷180+1=
+1=
（小时）
②当甲车停留在C地时，
÷60
=240÷6
=4（小时）
③两车都朝A地行驶时，
设乙车出发x小时后两车相距120千米，
则60x﹣[120（x﹣1）﹣360]=120，
所以480﹣60x=120，
所以60x=360，
解得x=6．
综上，可得乙车出发
小时、4小时、6小时后两车相距120千米．
故答案为：60、3．
