ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§≈ΉΈοœΏLΘΚy=x2-4x+3”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§ΕΞΒψΈΣCΘ°
Θ®1Θ©«σΒψCΚΆΒψAΒΡΉχ±ξΘ°
Θ®2Θ©Ε®“εΓΑLΥΪ≈ΉΆΦ–ΈΓ±ΘΚ÷±œΏx=tΫΪ≈ΉΈοœΏLΖ÷≥…ΝΫ≤ΩΖ÷Θ§ Ήœ»»ΞΒτΤδ≤ΜΚ§ΕΞΒψΒΡ≤ΩΖ÷Θ§»ΜΚσΉς≥ω≈ΉΈοœΏ Θ”ύ≤ΩΖ÷ΙΊ”Ύ÷±œΏx=tΒΡΕ‘≥ΤΆΦ–ΈΘ§ΒΟΒΫΒΡ’ϊΗωΆΦ–Έ≥ΤΈΣ≈ΉΈοœΏLΙΊ”Ύ÷±œΏx=tΒΡΓΑLΥΪ≈ΉΆΦ–ΈΓ±Θ®ΧΊ±πΒΊΘ§Β±÷±œΏx=t«ΓΚΟ «≈ΉΈοœΏΒΡΕ‘≥Τ÷α ±Θ§ΒΟΒΫΒΡΓΑLΥΪ≈ΉΆΦ–ΈΓ±≤Μ±δΘ©Θ§
ΔΌΒ±t=0 ±Θ§≈ΉΈοœΏLΙΊ”Ύ÷±’“x=0ΒΡΓΑLΥΪ≈ΉΆΦ–ΈΓ±»γΆΦΥυ ΨΘ§÷±œΏy=3”κΓΑLΥΪ≈ΉΆΦ–ΈΓ±”–______ΗωΫΜΒψΘΜ
ΔΎ»τ≈ΉΈοœΏLΙΊ”Ύ÷±œΏx=tΒΡΓΑLΥΪ≈ΉΆΦ–ΈΓ±”κ÷±œΏy=3«ΓΚΟ”–ΝΫΗωΫΜΒψΘ§ΫαΚœΆΦœσΘ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘΚ______ΘΜ
ΔέΒ±÷±œΏx=tΨ≠ΙΐΒψA ±Θ§ΓΑLΥΪ≈ΉΆΦ–ΈΓ±»γΆΦΥυ ΨΘ§œ÷ΫΪœΏΕΈACΥυ‘Ύ÷±œΏ―ΊΥ°ΤΫΘ®x÷αΘ©ΖΫœρΉσ”“ΤΫ“ΤΘ§ΫΜΓΑLΥΪ≈ΉΆΦ–ΈΓ±”ΎΒψPΘ§ΫΜx÷α”ΎΒψQΘ§¬ζΉψPQ=AC ±Θ§«σΒψPΒΡΉχ±ξΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©CΘ®2Θ§-1Θ©Θ§AΘ®1Θ§0Θ©ΘΜΘ®2Θ©ΔΌ3Θ§ΔΎ0ΘΦtΘΦ4Θ§ΔέΘ®![]() +2Θ§1Θ©ΜρΘ®-
+2Θ§1Θ©ΜρΘ®-![]() +2Θ§1Θ©ΜρΘ®-1Θ§0Θ©
+2Θ§1Θ©ΜρΘ®-1Θ§0Θ©
ΓΨΫβΈωΓΩ
Θ®1Θ©Ννy=0ΒΟΘΚx2-4x+3=0Θ§»ΜΚσ«σΒΟΖΫ≥ΧΒΡΫβΘ§¥”ΕχΩ…ΒΟΒΫAΓΔBΒΡΉχ±ξΘ§»ΜΚσ‘Ό«σΒΟ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣx=2Θ§ΉνΚσΫΪx=2¥ζ»κΩ…«σΒΟΒψCΒΡΉίΉχ±ξΘΜ
Θ®2Θ©ΔΌ≈ΉΈοœΏ”κy÷αΫΜΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ§»ΜΚσΉω≥ω÷±œΏy=3Θ§»ΜΚσ’“≥ωΫΜΒψΗω ΐΦ¥Ω…ΘΜΔΎΫΪy=3¥ζ»κ≈ΉΈοœΏΒΡΫβΈω Ϋ«σΒΟΕ‘”ΠΒΡxΒΡ÷ΒΘ§¥”ΕχΩ…ΒΟΒΫ÷±œΏy=3”κΓΑLΥΪ≈ΉΆΦ–ΈΓ±«ΓΚΟ”–3ΗωΫΜΒψ ±tΒΡ»Γ÷ΒΘ§»ΜΚσΫαΚœΚ· ΐΆΦœσΩ…ΒΟΒΫΓΑLΥΪ≈ΉΆΦ–ΈΓ±”κ÷±œΏy=3«ΓΚΟ”–ΝΫΗωΫΜΒψ ±tΒΡ»Γ÷ΒΖΕΈßΘΜΔέ Ήœ»÷ΛΟςΥΡ±Ώ–ΈACQPΈΣΤΫ––ΥΡ±Ώ–ΈΘ§”…Ω…ΒΟΒΫΒψPΒΡΉίΉχ±ξΈΣ1Θ§»ΜΚσ”…Κ· ΐΫβΈω ΫΩ…«σΒΟΒψPΒΡΚαΉχ±ξΘ°
Θ®1Θ©Ννy=0ΒΟΘΚx2-4x+3=0Θ§ΫβΒΟΘΚx=1Μρx=3Θ§
ΓύAΘ®1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§
Γύ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣx=2Θ§
ΫΪx=2¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚy=-1Θ§
ΓύCΘ®2Θ§-1Θ©ΘΜ
Θ®2Θ©ΔΌΫΪx=0¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚy=3Θ§
Γύ≈ΉΈοœΏ”κy÷αΫΜΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ§
»γΆΦΥυ ΨΘΚΉς÷±œΏy=3Θ§
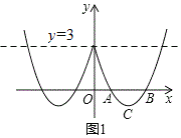
”…ΆΦœσΩ…÷ΣΘΚ÷±œΏy=3”κΓΑLΥΪ≈ΉΆΦ–ΈΓ±”–3ΗωΫΜΒψΘ§
Ι ¥πΑΗΈΣΘΚ3ΘΜ
ΔΎΫΪy=3¥ζ»κΒΟΘΚx2-4x+3=3Θ§ΫβΒΟΘΚx=0Μρx=4Θ§
”…Κ· ΐΆΦœσΩ…÷ΣΘΚΒ±0ΘΦtΘΦ4 ±Θ§≈ΉΈοœΏLΙΊ”Ύ÷±œΏx=tΒΡΓΑLΥΪ≈ΉΆΦ–ΈΓ±”κ÷±œΏy=3«ΓΚΟ”–ΝΫΗωΫΜΒψΘ§
Ι ¥πΑΗΈΣΘΚ0ΘΦtΘΦ4Θ°
Δέ»γΆΦ2Υυ ΨΘΚ
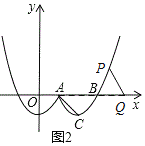
ΓΏPQΓΈAC«“PQ=ACΘ§
ΓύΥΡ±Ώ–ΈACQPΈΣΤΫ––ΥΡ±Ώ–ΈΘ§
”÷ΓΏΒψCΒΡΉίΉχ±ξΈΣ-1Θ§
ΓύΒψPΒΡΉίΉχ±ξΈΣ1Θ§
ΫΪy=1¥ζ»κ≈ΉΈοœΏΒΡΫβΈω ΫΒΟΘΚx2-4x+3=1Θ§ΫβΒΟΘΚx=![]() +2Μρx=-
+2Μρx=-![]() +2Θ°
+2Θ°
ΓύΒψPΒΡΉχ±ξΈΣΘ®![]() +2Θ§1Θ©ΜρΘ®-
+2Θ§1Θ©ΜρΘ®-![]() +2Θ§1Θ©Θ§
+2Θ§1Θ©Θ§
Β±ΒψPΘ®-1Θ§0Θ© ±Θ§“≤¬ζΉψΧθΦΰΘ°
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡΒψΘ®![]() +2Θ§1Θ©ΜρΘ®-
+2Θ§1Θ©ΜρΘ®-![]() +2Θ§1Θ©ΜρΘ®-1Θ§0Θ©
+2Θ§1Θ©ΜρΘ®-1Θ§0Θ©

 ΟœΫ®ΤΫΟϊ–ΘΩΦΨμœΒΝ–¥πΑΗ
ΟœΫ®ΤΫΟϊ–ΘΩΦΨμœΒΝ–¥πΑΗ