题目内容
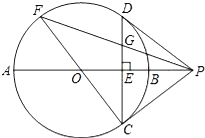
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC=![]() ,求EG的长.
,求EG的长.
【答案】(1)PD与⊙![]() 相切于点
相切于点![]() .(2)
.(2)![]()
【解析】试题分析:(1)连接OD,欲证PD是![]() 的切线,只需证明
的切线,只需证明![]() 即可,通过全等三角形
即可,通过全等三角形![]() 的对应角
的对应角![]() 来证明该结论.
来证明该结论.
(2)作![]() 于点M ,先求得
于点M ,先求得![]() ,从而求得
,从而求得![]() ,得出
,得出![]() ,然后证得
,然后证得![]() ,得出
,得出![]() .
.
![]() 中,
中, ![]() ,设
,设![]() ,
, ![]() ,则OC=3
,则OC=3![]() ,进而得出
,进而得出![]() ,从而求的
,从而求的![]() ,
, ![]() ,通过
,通过![]() 得出
得出![]() ,即可求得EG.
,即可求得EG.
试题解析:
(1)证明:联结![]()
∵在⊙![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
,
∴![]() .又∵
.又∵![]() ,∴
,∴![]() ≌
≌![]() .
.
∴![]() .
.
又∵![]() 切⊙
切⊙![]() 于点
于点![]() ,
, ![]() 为⊙
为⊙![]() 半径,
半径,
∴![]() ..
..
∴![]() .∴
.∴![]() .∴
.∴![]() 于点
于点![]() .
.
∴PD与⊙![]() 相切于点
相切于点![]() .
.
(2)作![]() 于点
于点![]() .
.
∵![]() ,
, ![]() 于点
于点![]() ,∴
,∴![]() ,
, ![]() .∴
.∴![]() .
.
∵![]() ,∴Rt△OCE中,
,∴Rt△OCE中, ![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() ,
, ![]() .
.
又∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() ≌
≌![]() .∴
.∴![]() ,
, ![]() .
.
∵在Rt△OCE中, ![]() ,设
,设![]() ,∴
,∴![]() .
.
∴![]() ,
, ![]() .∴
.∴![]() .∴
.∴![]() ,
, ![]() .
.
又∵![]() ,∴
,∴![]() ∥
∥![]() .
.
∴![]() ∽
∽![]() .∴
.∴![]() ,即
,即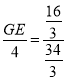 .
.
∴![]() .
.


练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目