题目内容
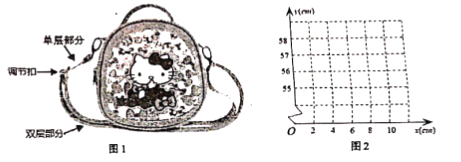
【题目】如图1是某品牌的一款学生斜持包，其挎带由单层部分、双层部分和调节扣组成.设单层部分的长度为xcm，双层部分的长度为ycm，经测景，得到如下数据：
x（cm） | 0 | 4 | 6 | 8 | 10 | … | 120 |
y（cm） | M | 58 | 57 | 56 | 55 | … | n |
(1)如图2，在平面直角坐标系中，以所测得数据中的x为横坐标，以y为纵坐标，描出所表示的点，并用平滑曲线连接，并根据图象猜想求出该函数的解析式；
(2)若小花要购买一个持带长为125cm的斜挎包，该款式的斜挎包是否满足小花的需求？请说明理由，(挎带的总长度=单层部分长度+双层部分长度，其中调节扣的长度忽略不计)
【答案】（1）见解析；
；（2）该斜挎包不能满足小花的要求，见解析.
【解析】
（1）根据表格中数据描点画图，根据图象猜想此函数为一次函数，用待定系数法可求出函数解析式；
（2）根据题意可得x+y=125，结合（1）中解析式列方程求解即可.
解：(1)画图如下；
；
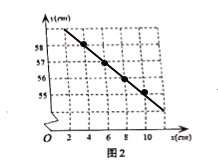从图表可知，此函数为一次函数，设此一次函数解析式为y=kx+b
依题意得
解得
，b=60,
∴该函数的解析式为
经检验，表格中的数据都满足该解析式.
(2)由①得：
∵x+y=125，
∴
解得x=130，
∵130>125
∴该斜挎包不能满足小花的要求.
练习册系列答案
口算能手系列答案
相关题目
