题目内容
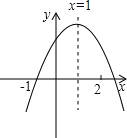
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

【答案】(1)h=﹣5t2+20t;(2)小球飞行3s时的高度为15米;(3)小球的飞行高度不能达到22m.
【解析】
(1)设h与t之间的函数关系式为h=at2+bt(a≠0),然后再根据表格代入t=1时,h=15;t=2时,h=20可得关于a、b的方程组,再解即可得到a、b的值,进而可得函数解析式;
(2)根据函数解析式,代入t=3可得h的值;
(3)把函数解析式写成顶点式的形式可得小球飞行的最大高度,进而可得答案.
解:(1)∵t=0时,h=0,
∴设h与t之间的函数关系式为h=at2+bt(a≠0),
∵t=1时,h=15;t=2时,h=20,
∴![]() ,
,
解得![]() ,
,
∴h与t之间的函数关系式为h=﹣5t2+20t;
(2)小球飞行3秒时,t=3(s),此时h=﹣5×32+20×3=15(m).
答:小球飞行3s时的高度为15米;
(3)∵h=﹣5t2+20t=﹣5(t﹣2)2+20,
∴小球飞行的最大高度为20m,
∵22>20,
∴小球的飞行高度不能达到22m.

【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)