题目内容
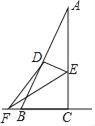
【题目】在RT△ABC中,BC=3,AC=4,点D,E是线段AB,AC上的两个动点(不与A,B,C重合)沿DE翻折△ADE使得点A的对应点F恰好落在直线BC上,当DF与RT△ABC的一条边垂直的时候,线段AD的长为_____.
【答案】![]() 或
或![]()
【解析】
设AD=DF=x,则BD=5﹣x,分两种情况讨论:DF⊥BC,DF⊥AB,依据相似三角形的对应边成比例,即可得到比例式,进而得出DF的长.
∵Rt△ABC中,BC=3,AC=4,
∴AB=5,
设AD=DF=x,则BD=5﹣x,
①如图,当DF⊥BC时,∠DFB=∠ACB=90°,
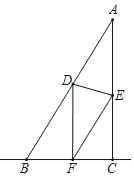
∴AC∥DF,
∴△ABC∽△DBF,
∴![]() ,即
,即![]() ,
,
解得x=![]() ;
;
②如图,当DF⊥AB时,∠ACB=∠BDB=90°,而∠ABC=∠FBD,
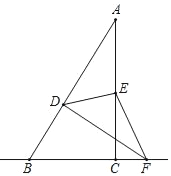
∴△ABC∽△FBD,
∴![]() ,即
,即![]() ,
,
解得x=![]() ;
;
综上所述,线段AD的长为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
计算方差的公式:s2=![]() [(x1-
[(x1-![]() )2+(x2-
)2+(x2-![]() )2++(xn-
)2++(xn-![]() )2]
)2]