题目内容
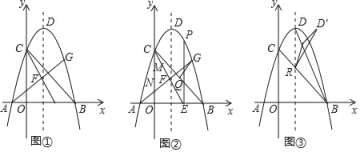
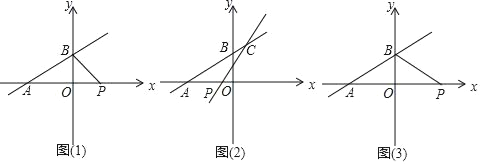
【题目】如图1,在Rt△AOB中,∠AOB=90°,∠OAB=30°,点C在线段OB上,OC=2BC,AO边上的一点D满足∠OCD=30°.将△OCD绕点O逆时针旋转α度(90°<α<180°)得到△OC′D′,C,D两点的对应点分别为点C′,D′,连接AC′,BD′,取AC′的中点M,连接OM.
(1)如图2,当C′D′∥AB时,α= °,此时OM和BD′之间的位置关系为 ;
(2)画图探究线段OM和BD′之间的位置关系和数量关系,并加以证明.
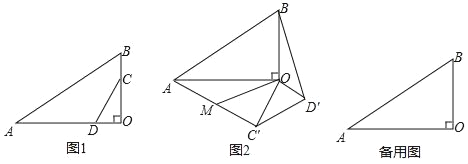
【答案】(1)150,垂直;(2)OM⊥BD′,OM=![]() BD′
BD′
【解析】
(1)根据平行线的性质得到∠ABD′+∠C′D′B=180°,
根据周角的定义即可得到结论;
(2)取AO的中点E,连接ME,延长MO交BD′于N,根据三角形的中位线的性质得到EM∥OC′,EM=![]() OC′,根据相似三角形的性质得到∠AOM=∠2,
OC′,根据相似三角形的性质得到∠AOM=∠2,![]() ,根据垂直的定义即可得到结论.
,根据垂直的定义即可得到结论.
解:(1)∵C′D′∥AB,
∴∠ABD′+∠C′D′B=180°,
∵∠ABO=∠C′D′O=60°,
∴∠OBD′+∠BD′O=60°,
∴∠BOD′=120°,
∴∠BOC′=360°﹣90°﹣90°﹣120°=150°,
∴α=150°,此时,OM⊥BD′;
故答案为:150,垂直;
(2)OM⊥BD′,OM=![]() BD′,
BD′,
证明:取AO的中点E,连接ME,延长MO交BD′于N,
∵AC′的中点M,
∴EM∥OC′,EM=![]() OC′,
OC′,
∴∠OEM+∠AOC′=180°,∵∠AOB=∠C′OD′=90°,
∴∠BOD′+′AOC′=180°,
∴∠OEM=∠BOD′,
∵∠OAB=∠OC′D′=30°,
∴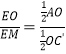 =
=![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
∴△EOM∽△OBD′,
∴∠AOM=∠2,![]() ,
,
即OM=![]() BD′,
BD′,
∵∠AOB=90°,
∴∠AOM+∠3=180°﹣∠AOB=90°,∴∠2+∠3=90°,
∴OM⊥BD′.

【题目】某童装专卖店,为了吸引顾客,在“六一”儿童节当天举办了甲、乙两种品牌童装有奖酬宾活动,凡购物满100元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同.摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如表).
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的童装?并说明理由.
甲种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 15 | 30 | 15 | |
乙种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 30 | 15 | 30 |
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .