Question

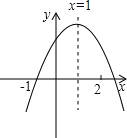
【题目】已知二次函数的图象如图所示，有下列结论：①abc＜0；②a+c＞b；③3a+c＜0；④a+b＞m（am+b）（其中m≠1），其中正确的结论有______．

Answer 1

【答案】①③④．

【解析】解：①由图象可知：a＜0，c＞0，∵ ＞0，∴b＞0，∴abc＜0，故此选项正确；

②当x=﹣1时，y=a﹣b+c＜0，故a+c＞b，错误；

③当x=3时函数值小于0，y=9a+3b+c＜0，且x==1，即b=﹣2a，代入得9a﹣6a+c＜0，得3a+c＜0，故此选项正确；

④当x=1时，y的值最大．此时，y=a+b+c，而当x=m时，y=am2+bm+c，所以a+b+c＞am2+bm+c，故a+b＞am2+bm，即a+b＞m（am+b），故此选项正确．

故③④正确．

故答案为：①③④．